https://senseis.xmp.net/?MostSimilarProGame
The record is apparently 73 identical moves, in the game pair Fujisawa Hosai – Go Seigen 1957 / Fujisawa Hosai – Rin Kaiho 1965, manego games.
Note, though, that that article last got edited in 2006.
6 Likes
27 moves, from Qiu–Wang and Ge–Zhu, both 1996.
27 moves, from Lee-Wang 2010 and Han–Ahn 2011.
21 moves, from Lee–Jang 1989 and Hong–Ha 1992.
21 moves, from Cho–Lee and Ha–Kim, both 1992.
3 Likes
Yeah - at first 78 seems like “wow, inconceivable”, but when you think about joseki, basic strategy (that we learn and copy from pros), and everyone learning pro games themselves specifically in order to “play like that”, then it’s not so unlikely. I can easily imagine Dwyrin “Basic Series” adherents playing similar openings up to ~ move 40, so that would be the “starting point” even for Kyus baseline similarity…
3 Likes
well, you say that, but a lot of recent pro games seem to diverge at around move 20 or so from all the games in waltheri with all natural moves (well, if you consider AI joseki normal at this point) – Also you’ll notice that the diagram in the example for 78 started out with some amount of mirror go between the same two players with what seem to be rather long corner joseki sequences
2 Likes
I’m not too clear about the point you’re making. The construction “well you say that but” seems to imply a contradiction follows, but your points seem to confirm what I was saying.
Statistically, but dreadfully loosely, if the “mode” for divergence is as high as 20, then this in itself hints that 78 is not really inconceivable. What is the tail like … it would not have to be very “long and fat” to put the probability of 78 as “conceivable”.
Then the idea that strategies like “mirror” will increase the chances of games matching only increases the sense we get that long strings of matches are actually quite conceivable.
Which all seems to mean that it could well be that to be sure of being unique you need to be approaching 100 moves!
2 Likes
I don’t think this follows from the earlier sections: logically you cannot “be 100% sure” that there is no other game (without an explicitly made collection of games to reference) ever stops following the same path. There is the possibility that entire 300+ moves-long game has a duplicate somewhere else within human experience
We can only work in confidence intervals (a couple favorites being the p-values rising from 2, 3, and 5 standard deviatiosn), for which we also have to consider that while kyus many times “follow what the pros do”, they are also very bad at trying to follow what the pros do, and in a smaller data set are more likely to diverge from the pros quickly (and maybe each other), so it would stand to reason that it could follow a distribution where 78 is beyond our chosen interval of confidence for amateur games.
I think just 1 or 2 moves should be enough. I mean, just play the first move at 9-8 or something. Even if someone already played there before, because of the rarity of 9-8 first move, the 2nd move will likely make the game unique.
2 Likes
If 2 players often play with each other
and both review their games with bot
both remember where they played until “not bot” move
Then their games will be identical in the beginning until farther and farther move.
And then after hundred or so games, they always will play same game until the end, which is identical to bot vs bot game.
The one who review their games with stronger bot, wins.
There might be a good way to make an estimate of this, since as stated by the original poster on post 9 we wanted to hone in on pro games, if we analyze enough positions, we can find the average “information rate” of each move (ofc, this method treats all time periods and portions of the game as independent which may not be ideal) by the typical formula for shannon entropy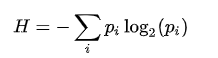 
(where H is entropy, and pi is the probability of event i), which has a neat property of being potentially reversible into a percentage and it being based on logarithms turns a lot of multiplication questions into ones of addition.
How this would work is you take the shannon entropy for each position analyzed (which is the average information granted by games that passed through the position), and with a lot of these positions, you can average these entropies together additively to create an “average entropy of every position within pro games”. We’ll call this A. One of the nice things about A is that for a position that is m moves deep, the amount of information probably gained in bits (according to this model) is m * A. we can then reverse the logarithm to output a probability via 2 ^ (- m * A), which is the probability that a game in the dataset would reach this position, that we’ll call q. With q and the number of games in the data set N, we can then calculate that the probability that there is no other game that reached the same position is (1 - q) ^ N, and the probability of the opposite being 1 - (1-q) ^ N, which then you can then compare to your chosen confidence threshold.
This is, informally, what I was doing. I never said I was “100% sure” that a game is unique at any point. Rather, I was answering the actual question, which is “when does a game become unique statistically”.
I asserted that the very qualitative (“deadfully loosely”) input that we had made me feel that, contrary to my initial gut feel, the answer was going to be quite a large number, for the reasons I outlined.
I took this approach because I’m not equipped to do real statistical analysis of this kind
, but I was struck by the suprising nature of what we are seeing - the small set of data in this thread - and wanted at least some sort of insight that I could understand into it.
I think your gut feel (that games are unique after a relatively short time?) is still valid. A 78 move game is quite impressive, but the mode seems to be way less than that (did we land in the 20s?)
1 Like
When I experiment a bit in Waltheri’s, in many position the top 2-ish moves are played in about 90% of games from that position.
So each pro move roughly halves the number of pro games played from that position. That database has about 50,000 games, so about log2 50,000 ~ 16 moves would be an estimate for the mode of uniqueness in Waltheri’s.
If instead we take 1.5 as a typical “branching factor” for pro games, we get log1.5 50,000 ~ 27 moves as an estimate for the mode of uniqueness in Waltheri’s.
5 Likes
We could attempt a “dumb estimate” to get our footing.
Let T be the total number of games of Go ever played.
T(low) = 1,000,000,000 (1b); T(mid) = 10,000,000,000 (10b), and T(high) = 100,000,000,000 (100b).
Let P be the average number of playable moves in each position.
P(low) = 2, P(mid) = 3, and P(high) = 5.
Let D be the move of uniqueness, if all branches have an equal number of games.
We can say that D is the smallest number that fits the equation P ^ D >= T for each set, and set about finding it.
| T | P | D | Equation |
|---|---|---|---|
| low | low | move 30 | 2 ^ 30 > 1b |
| low | mid | move 19 | 3 ^ 19 > 1b |
| low | high | move 14 | 5 ^ 14 > 1b |
| — | |||
| mid | low | move 34 | 2 ^ 34 > 10b |
| mid | mid | move 21 | 3 ^ 21 > 10b |
| mid | high | move 15 | 5 ^ 15 > 10b |
| – | |||
| high | low | move 37 | 2 ^ 37 > 100b |
| high | mid | move 24 | 3 ^ 24 > 100b |
| high | high | move 16 | 3 x 16 > 100b |
Range: move 14 – move 37
4 Likes
[the Waltheri] database has about 50,000 games
It has 79,815 self-declared games, which is closer to 100,000.
IIRC, the GoGoD database has at least 130,000 professional games.
1 Like
Oops, so I should add about 1 or 2 moves to my estimates.
1 Like
You’re estimating that something like half of the games in Waltheri aren’t unique until over 25 moves?
In my experience, it’s not trivial to find any games there that are still non-unique at that point.
1 Like
To find the less unique games, you need to select one of the top 2 moves all the time, or just the #1 move if it is much more popular than #2.
To find games that are unique early, you need to select the unpopular moves all the time.
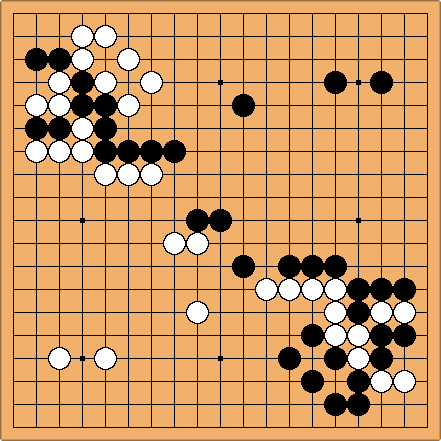
This is the widest path on Waltheri, ie. the position reached by picking the most popular move every single time from the very beginning.
Uniqueness is attained on the twenty-fourth move (Chen–Zhou 2008 / Takano–Kobayashi 2009).
5 Likes
My estimate is that pro game uniqueness is likely to occur somewhere between move 16 and move 29 (let’s round to 15 and 30 for simplicity) for pro games.
This is by using a branching factor of 1.5 - 2 for about 100k pro games.
You got similar estimates with a branching factor of 2 - 5 for about 1G amateur games.
2 Likes
Do you think 22 is a fairly accurate professional uniqueness median, then?