Also red
1 Like
My current hypothesis is “there exist two black stones with manhattan distance >= 6”
needless to say, my confidence is low 
2 Likes
But I cannot construct a green counterexample 
Edit: I could after all construct one: 
6 Likes
Is the rule defined for 7×7 boards only?
Variations of #419:
1 Like
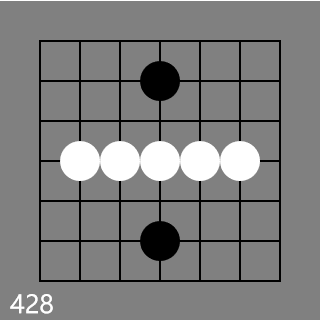
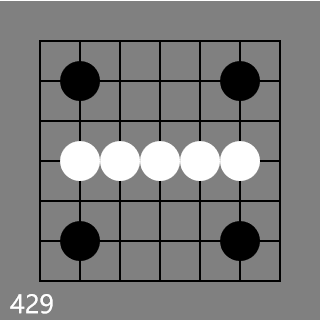
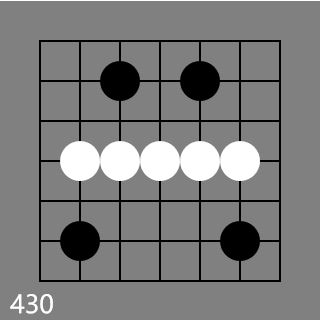
428 has to be red, otherwise it would be a green counterexample for
This information is very valuable for us. We know all green Koans have two black stones with manhattan distance >= 6.
3 Likes
2 Likes
I would like to test how far we can push the limits of the five-white-in-a-row series (#419, #433, #434; #431) subject to @martin3141’s constraint.
1 Like
1 Like
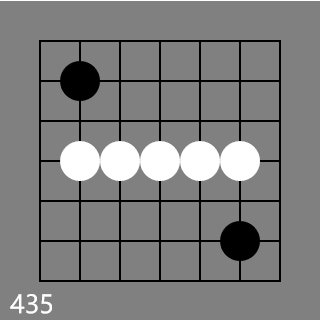
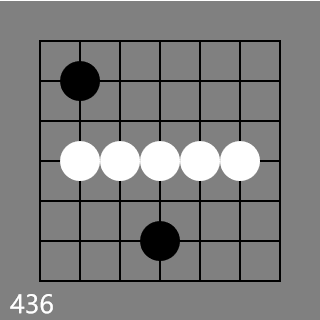
I made a mistake. With some more thought, here is a green counter example:
5 Likes
I’m wondering if the property depends on all three of the Black stones.
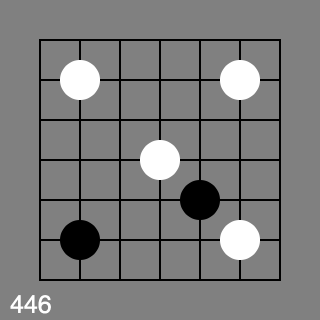
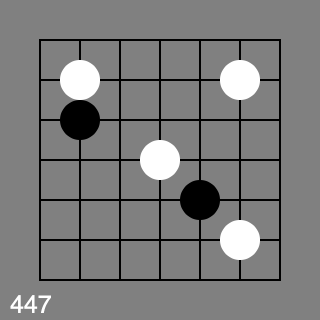
I’m also wondering if it depends on the White stones
1 Like
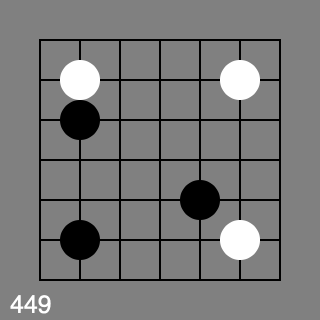
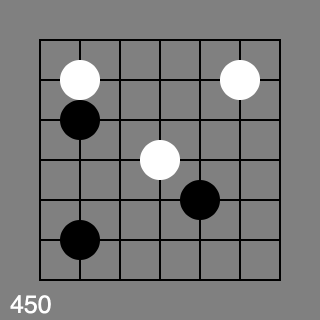
Ok, 445,446 and 447 are all red. 448 - 452 are all green
2 Likes
Interesting…
That seems to suggest that this should also be green:
2 Likes
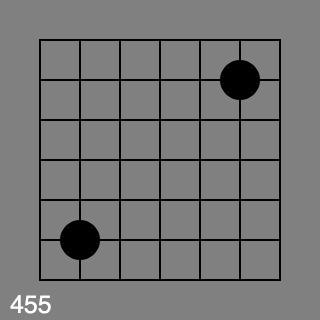
correct
1 Like
I’ll add them to your first post
Oh that’s why I got an error when editing the post 
Now we both did the work
2 Likes
Teeheehee
My expectation is that this koan is green:
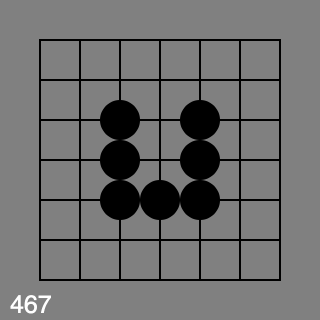
and this koan is red:
2 Likes
1 Like
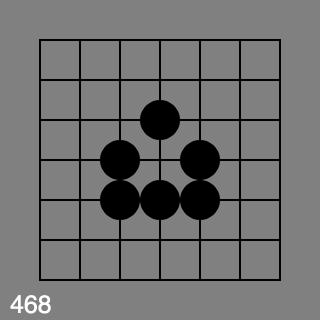
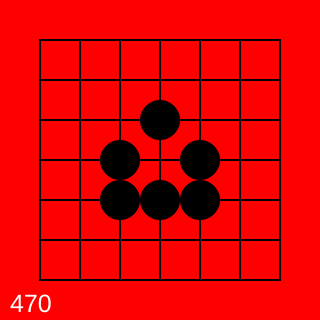
So much for my hypothesis, then
2 Likes
These results seem to indicate that the rule (maybe) does not distinguish between white stones and empty intersections.
My current hypothesis is
Spoiler
“The smallest rectangle including all black stones has at least 16 intersections.”
Once again I’m not very confident, but seems to work for the Koans so far 
@UrbanSpirit please feel free to ignore this hypothesis, its just for discussion purpose and not an official rules guess.
3 Likes