How does OGS avoid negative ratings?

General Chat
21

Well what I’m saying is that if one player always has a precisely 0% chance of winning against another player, it can’t properly fit within a rating system that always predicts a nonzero chance of winning and still have accurate predictions for win rates.

You can put them in the rating system, we can put the random-move-nixbot of the OP into the Glicko or Elo rating system.

What I’m saying though is that if it genuinely had a 0% chance of winning against other players, its rating will always be innaccurate. The system like Glicko or Elo will always overpredict how many games it would win, given a large enough sample set of games.

Is that inherently a wrong statement?

There’s two different points here, one is just having a rating system and being able to assign numbers to players, and one is whether the rating system actually predicts correctly the results of accurately rated players. You can always put any two players into the same system, but whether that system is better than a random number generator at predicting the result of a game, given the two numbers is the actual meaning of the ratings. That rating difference somehow translates to skill in the game.

22

If you’re playing against bots, how often do they resign on your move?

Bots typically treat resigning as a legal move, so resigning on your opponents turn would be illegal.

So maybe bots playing Go is already a go variant.

2 Likes
23

I suppose I can concede that since many games have a finite number of positions and a finite number of moves you can play in those positions, then even a uniform at random player can’t have a 0% chance of winning against any player.

4 Likes
24

At these extreme cases, I think in practice there are already other limits that we run into.

Elo ratings will asymptotically approach a value in the right ballpark, given an infinite number of games and infinite precision in its rating calculations.

But at a more realistic ~10 digits of precision, the winning chance for a skill gap of 4000 Elo is already 0.000000000. So the rating of the worst player of a rating population won’t drop more than 4000 points below the rating of the 2nd worst player of that rating population, however many games they play.

Indeed, their actual rating gap could be much bigger, but in pactice it hardly makes a difference, because the underprediction of the win chance is less than 0.0000000005.
Even with infinite precision calculations it may take many billions of games to determine how much bigger their skill gap really is (or equivalently, where exactly the first non-zero digit is in that win chance), and most players (even bots) play much less than billions of games in their active playing lifetimes.

Also, there is random noise all over a normal rating population, so ratings are never 100% accurate, even when rating calculations use infinite precision in their calculations.

2 Likes
25

My intuition would be the the heat death of the universe would happen before a bot playing random moves beat Katago, even though it’s technically “possible”

1 Like
26

Deepmind estimated AlphaGo Zero’s Elo rating at about 5000 points. If a random player would have an Elo rating of about -3000 points, the Elo system would predict a winrate of about 1E-20. If they would play 1 game per hour, it would probably take about 1E16 years before the random player wins its first game (and thus establish a rating gap of about 8000 points).

Heat death is much, much further away at around 1E1000 years.
Already the Dark Era (when even supermassive black holes will have evaporated) is much further away at around 1E100 years.

Though 1E16 years would be (way?) past the last star formations, which is estimated at around 1E15 years.

A much more practical and much less time consuming method to determine the rating gap between these extremes, is to have many players in between participating in the rating system (like filling up the gap with players spaced by 100 rating points), and assume transitivity of Elo rating gaps.

4 Likes
27

Guess my intuition was wrong

2 Likes
28

What should be 480?
Also I don’t understand what that 2011 article has to do with this topic of very low ratings. In that article, Sonas seems to be saying that he was wrong in 2002, when he proposed some cutoff in the winrate prediction formula that the FIDE uses. And the article doesn’t mention the number 480.

29

Not sure why they would do that since it’s been shown to be inaccurate.

30

“apply a 5/6 scaling factor to all the rating differences”
Oops. I inflated the 400 demonimator instead of shrinking the rating difference thinking it was functionally the same thing. I was thinking 400 is 5/6 of 480.

31

Aha, I get it now. You’re talking about systematic underpredictions of winrates in FIDE rated games between lower rated and higher rated players, which Sonas pointed out in 2002:

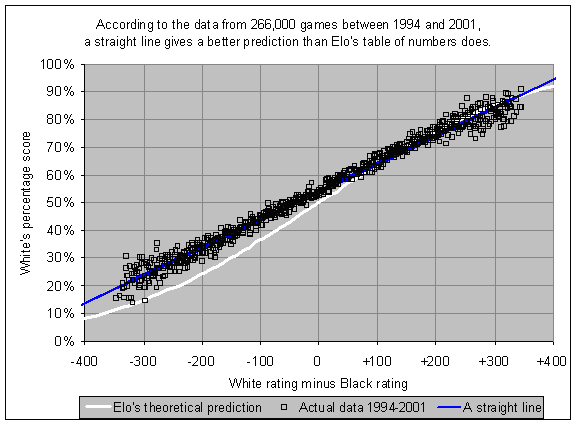
In 2011 he points out that this can be fixed by adjusting the Elo formula a bit. Instead of defining a 400 rating gap as corresponding to 1:10 odds, it could define a 480 rating gap as corresponding to 1:10 odds, and then the predictions would fit the observations:

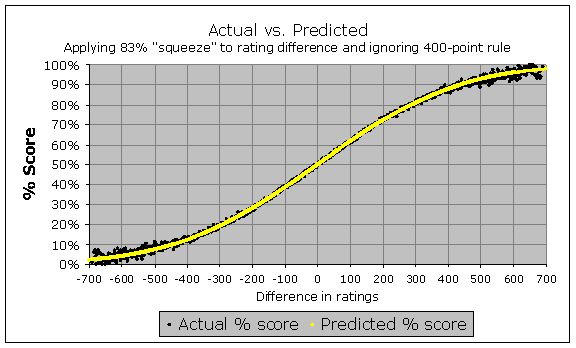
While this may “work” in the case of these FIDE rated games, it does feel like a hack to me. It’s like ad hoc adjusting all weather forecasts 2 degrees downward to make it fit observations better.
Instead of applying such a hack, I think it would be better to investigate what might be causing the discrepancy. Perhaps adjusting some other parameters in the system would also fix the issue, while having a better theoretical basis than the hack.

For instance, the observations show that lower rated players tend to win more often against higher rated players than predicted from the rating difference. This could be caused by a tendency of lower rated players to be systematically underrated. And that could be caused by ratings of upcoming lower rated players catching up too slowly to track their actual improvement. And that could be caused by the K factor of these games being too small and/or by a lack of sufficient rating point injections into the system to prevent deflation from improving players.

I don’t know if those hypotheses are actually true for FIDE ratings, but I think it’s worth it to investigate those and potentially counter root causes for the issue, rather than applying the proposed hack.

Now, I don’t think EGF ratings have such a systematic discrepancy, at least not anymore since the 2021 retroactive update of the EGF rating system. (EGF ratings are not Elo ratings, but under the hood the EGF rating system actually does use the Elo algorithm on implied Elo ratings).

I was heavily involved in preparing that update and it was apparent to me that the original conversion had a prediction mismatch similar (much worse even) to what Sonas observed in FIDE ratings [1].
So I specifically aimed at shaping the Elo to rank conversion such that the winning predictions matched winning observations as closely as possible with a rather simple formula, see the β function at https://www.europeangodatabase.eu/EGD/EGF_rating_system.php#System. Together with some other parameter adjustments (such as the K factor and anti-deflationary rating point injections into the system), this resulted in a much better match between predicted and observed winrates [2].

As far as I understand, OGS did a similar thing (although perhaps not as elaborate) in its most recent major rating system update a couple of years ago.

[1] (before the update)
Note that the ratings on the horizontal axis are EGF ratings, not Elo ratings

image
image1162×621 180 KB

image
image1163×618 167 KB

[2] (after the update)
Note that the ratings on the horizontal axis are EGF ratings, not Elo ratings

image
image1163×619 180 KB

image
image1163×620 175 KB

1 Like
32

There was an interesting comment in a 2020 article

And I think the most important insight of all is this: the FIDE Elo rating pool is too stretched out. This has the result of exaggerating the true difference in strength between any two players, and so the expected score is calculated to be further from 50% than it really should be. And this is a very difficult problem to solve. It cannot be solved by simply adjusting the Elo Expectancy Table; if we did that, then the ratings would respond accordingly and we would be in the same boat again. It is much trickier to solve than that.

The part that I don’t understand is

why this would be a hack, and as they seems to suggest, it wouldn’t work in practice supposedly.

Let’s say the original formulae for rating are supposed to be a best guess at skill and winrate prediction in chess.

That is the rating system, Elo system say, is supposed to suggest that if we can assign players these numbers and those numbers are accurate, then we should see certain predicted winrates between these players.

Then you let the system settle for a while so players sit at their ratings in the system, and it turns out the predicted winrates are wrong.

Why is it a hack to say that “yes our initial parameters in the model don’t model chess skill as accurately as these other parameters do”.

As in if you change the 400 to something else and it fits the data better, is that not simply saying that this is how it should be for chess, and our initial rounded guess of the number 400 was a bit off?

It seems like he’s saying that if you adjust this number, the system will recalibrate over time, player will gain or lose some points in tournaments and settle at new ratings. The assumption is then that it will still be off for some reason I don’t understand.

Or is it that they’re assuming that it must be another effect that’s at play, and hence just adjusting the parameters won’t fix that effect.

1 Like
33

Like I said, there are other factors in the system that affect a player’s rating evolution, and thus their current rating.

When you observe that winrate predictions from a rating difference don’t match observations, it doesn’t necessarily mean that the prediction formula is wrong (if you assume this formula is the culprit, you basically doubt the core of the whole Elo rating system and you might as well throw it all in the bin).

Instead, you should also consider the possibility that the formula is correct, but somehow weaker players tend to be underrated by biases in the system. Like, perhaps the system didn’t reward them with as large a rating increase as it should have from good results in the recent past. This could be caused by using a too small K factor (I suppose Glicko was specifically designed to mitigate this).

You could test such a hypothesis by comparing observations of games between plateauing players with observations of games between upcoming players and plateauing players.
You could also test if recalculating the rating evolutions of the whole rating population with a larger K factor helps to achieve current ratings that result in a better match between predictions and observations.
When you have a testing system in place to recalculate the rating evolutions of the whole rating population and evaluate the results, you could also try some other ideas to mitigate an alleged rating lag of upcoming players.
Like, the EGF rating system has a mechanism of rating resets. It’s a rather crude mechanism, but it does help to mitigate rating lag of upcoming players. As far as I could tell from my tests at the time, it’s even indispensible for the EGF rating system (although it’s not quite enough in itself, because the mechanism tends to be underused, and its usage depends on the speed of a player’s progress and on the policies of a player’s national go association, like every low dan in Europe is scared of being pitted against a French 3k).
It’s possible that using Glicko instead would also work to mitigate rating lag of upcoming players, but I never tested that.

1 Like
34

If careful analysis shows no evidence of winrate discrepancy affecting upcoming players more than plateauing underdogs, I’d bring forward another hypothesis to explain why lower rated players do better than expected against higher rated players in FIDE rated games:

Perhaps it’s a psychological effect, where the underdog tries harder when playing against a higher rated player, causing them to actually play better? Or the higher rated player feels complacent when playing against a lower rated player, causing them to actually play worse?

This hypothesis might be tested by not letting players know their opponent’s rating before the game ends and seeing if those results match predictions better.

If the match would indeed be clearly better, that could be an argument to actually use the modified prediction formula when the players do know each other’s ratings before the game.
In that case adjusting the winrate prediction formula wouldn’t be an ad hoc fix anymore IMO.

Though you could still opt to keep the original formula, being satisfied that the discrepancy is explained by psychology, and realising that this does not affect everyone the same (and also consider that bots won’t be affected by this at all).

And perhaps it’s a bad idea to complicate the rating system with additional parameters (in this case a 5/6 constant) to compensate for various psychological factors and other stuff that could affect game results. Adding moving parts could make the system more accurate, but it could also add points of failure.