Am I the only one that always refused by the server?
Works for me (and it’s a miracle it does given my country is moving towards the china-like firewall)
But a website block by the Great Fire Wall doesn’t reply anything because of DNS poisoning. It looks like there’s something wrong with my request.
Summary
find p,q so that pq=500 and 0<p<q<2p
p=20,q=25
x=20,y=5
a=200,b=375,c=425
1 Like
Question
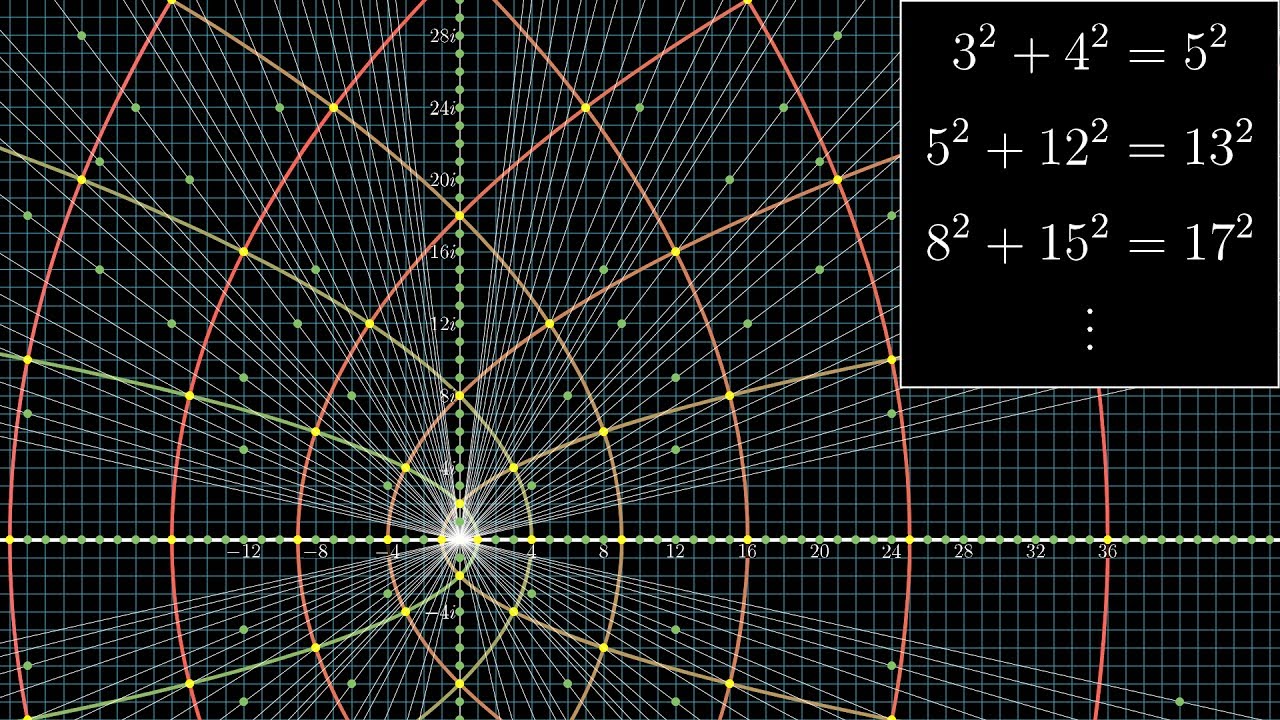
Is every pythagoreian triple of this form? ( c = x^2 + y^2, b = x^2 - y^2, a = 2xy )
Answer
If gcd(a,b,c)=1, I can prove it.
15^2=9^2+12^2 is not of this form. gcd(15,9,12)=3
1 Like
Okay something weird happened. I coded this:
prob 9, py
def tripletOfSum(N):
for m in range(N):
for n in range(N):
a = m**2 - n**2
b = 2*m*n
c = m**2 + n**2
if a+b+c == N:
return [a,b,c]
elif a+b+c > N:
break
print(tripletOfSum(1000))
Of course I have to multiply abc, but I wanted to see which triplet this will yield
And I got this result, which seems to checks out:
solution prob 9
[-249000, 998, 249002]
This seems to contradict @Glunkolin 's solution, which also seems to check out, as well as the problem’s claim that there is just one solution.
-249000 is not a natural number
2 Likes
ah, see, I missed that this was in the problem description, that explains it. That restricts the search space above to all triplets with m>n
that did the trick
working solution to 9, py
changed the range of the nested loop
def tripletOfSum(N):
for m in range(N):
for n in range(m):
a = m**2 - n**2
b = 2*m*n
c = m**2 + n**2
if a+b+c == N:
return [a,b,c,a*b*c]
elif a+b+c > N:
break
print(tripletOfSum(1000))
This video includes a pretty proof of this fact 
2 Likes
It feel like exposing there being only 1 triplet make the problem too easy isn't it? This problem can be solved with paper & pencil, but I still try to code
const solve = () => {
for (let a = 1; a <= 998; a++) {
for (let b = 1; b < 1000 - a; b++) {
const c = 1000 - a - b;
if (a * a + b * b == c * c) return a * b * c;
}
}
};
Final result: 31875000
Total time: 2 ms
3 Likes
Hmm last comment 4 days ago - can I make one up? 
Easy:
Imagine an alternate universe where everyone’s rank is unique, and higher ranked players always win against lower ranked players. In this alternate universe, you join a go club where the players know their relative ranks.
What are the minimum number of games you need to play in order to determine your relative rank in go club? Can you write a function to determine your relative rank in Go club, as expressed by the number of players in club who have a lower rank than you?
Example (note: absolute ranks are shown for the purposes of the example, but the members of the club do not know their absolute ranks): There is a go club that consists of Asami (1d), Benji (7k), and Chang-ho (9k). Your rank is 5k. When you join the club, you play against Benji and win. Then you play against Asami and lose. Therefore you know your relative rank is 2 because you are ranked higher than Benji and Chang-ho.
Hard:
Imagine a different alternate universe where everyone’s rank is an integer. Instead of always winning or losing, chances of winning or losing are probilistic (much like in real life):
rank diff | chance of stronger player winning 0 | 50% 1 | 75% 2 | 90% >3 | 100%How many games must you play in a new Go club to know your relative rank with >90% certainty?
I’m not so sure about the second problem… Do I need to provide the distribution ranks? If so, let’s assume that ranks are uniformly distributed in the range [0, 30).
Oh, and if there are any edits that would make these problems more clear, feel free to tweak them - I’ll make this a wiki.
4 Likes
easy bit
For N players, it’s just ld(N), rounded to the nearest integer, up or down by chance. You just look for the median player in the club, and if you win, you look for the median player of all stronger players, or vice versa for weaker players.
For the hard bit, it might be worth it to run some code, but we would need an optimal strategy first anyway. We need to maximize information gain, so for the first game we definitely have to look for the median opponent, so someone of rank 14. From there on it gets a bit trickier, since if we win, this reduces our possible relative rank to 0-16, however the uniform distribution is now messed up, so this must be taken into account when deciding which opponent to pick next for maximizing information gain.
1 Like
Yeah, at this point I think this question is a bit harder than hard (I’m not even sure how to answer it). I’m wondering if we can modify it to make it closer to medium-hard
I think it is possible. If we think of each individual rank having a probability of 1/30 (or any other distribution works as well), then each game alters the probability. For example, if we win, ranks 0-11 get multiplied by 1, 17-29 by 0, and then 12 by .9, 13 by .75, 14 by .5, 15 by .25 and 16 by .1. You can then get the probability of being a certain rank by dividing its probability by the sum of all remaining probabilities. You then have to iteratively find the closest thing to a median in your distribution, until one rank has a relative probability of more than 90%. This will certainly include playing the same opponent a few times over in the end.
1 Like
This made me curious about this follow-up to the easy question:
If we have n players with unique ranks, how many games are needed in the worst case to determine all the ranks? (assuming again that the stronger player always wins)
Since this is equivalent to minimizing comparisons in a sorting algorithm, I kind of expected there to be a definite answer out there, but it seems to be hard enough that it’s still an open problem:
(see both links in that answer for more info)
2 Likes
I think my problem is a bit closer to minimizing comparisons in a
Spoiler
binary search algorithm
I assume that’s a bit easier than sorting, as there’s pretty much one way to do that.
Here’s another question I had queued up along thos lines though.
You are organizing a tournament in the alternate universe, where everybody’s rank deterministically predicts who wins. You don’t know anybody rank going into the tournament.
What are the fewest number of games needed to determine the relative rankings of the players in this tournament?
1 Like
Isn’t your last question the same as the one I wrote? 
(which seems to be surprisingly very difficult)
2 Likes
Oh crap i misread, I thought you had quoted the original problem’s followup (“Can you write a function…”). No yeah that’s a dup i just cant read in the morning (7k here 
)
1 Like