It might actually not work on further examination.
There’s some precise wording, which makes me thing one might need to go to even bigger sizes to possibly make this idea work
It might actually not work on further examination.
There’s some precise wording, which makes me thing one might need to go to even bigger sizes to possibly make this idea work
This sounds fairly useful, I could’t think of how to formalise it with the parallel and perpendicular lines!
I’ll have to reread it a couple of times!
I actually made a mistake. It should be a circle instead of a square over the line segment.
Here is a picture that corresponds to my revised statement:
Given two points A and B, the open blue region (excluding the border lines) are the points C that result in an acute triangle ABC.
Oh right, I was having a look at the square and it seemed pretty cool
Oh but then on further consideration
there is that whole theorem that the angle in a semi circle is a right angle (if the grid point happens to lie on the semi circle. (Is that where the idea comes from?)
In case you are interested in this, there is a general theorem that is applicable for any chord (not just the diameter): Inscribed angle - Wikipedia
This would be my next attempt, doubling and then fudging the doubles to try to get around the problems
So it’s 36x36, replacing each pixel/square by a 2x2, except the perimeter.
So reading it to mean that “segment created” would have to be a segment that changes length with the flip.
Interestingly if you ask ai about the problem, it thinks the answer is
the answer is 32 stones
Why, no idea, I can’t imagine it anyway. (I think it might just be autocompleting to a random number ![]() )
)
I tried a bit of brute force searching, which came up with an 11 on size 5.
Still only found an 18 so far. The search space seems very big. I’d generate pairs, and for each pair add possible third points, then fourth points and so on.
I tried reducing the number of input pairs with symmetry, and dumping out a list of points, if the remaining candidates to add which don’t make acute angles, plus the ones in the list, are shorter in total than the longest found one so far.
It’s speeds up a bit, but not by much really. It spat out this thing for a size 18, which looks funky:
That (2,2) point looks particularly strange - I’ll have to stare at this a bit longer some other time to see if it makes sense.
I was trying different ideas of depth first search and breath first search with pruning, I think maybe breadth first is way too slow except on smaller boards when it was much faster.
Anyway, depth first came up with this one after a while with 19
I was using geogebra a bit to play around with the points and angles, just to see if I can understand if it works and why with the previous example - will probably do the same with this one for a bit.
Edit: E.g.
Oh, that’s a great solution! I would’ve bet on the maximum being 18
Just if anyone wanted to play about with it, or try to optimise it further (I didn’t finish the search, I don’t know how long it would take)
#go board 9x9 puzzle, acute triangles
# idea is to find the most number of stones on a go board that can be placed
# such that no three stones form an acute triangle
import numpy as np
# 9x9 board as points (i,j) with i,j in [1,9]
# generate list of all possible pairs of points on the board,
# then expand in a sort of tree search to find the maximum number of points
N=9
all_points = [[i,j] for i in range(1,N + 1) for j in range(1,N + 1)]
all_pairs = [[p1,p2] for p1 in all_points for p2 in all_points if p1 != p2]
def angle_at_point(p,q,r):
# given three points p,q,r, return the angle at q
# angle is in radians, in [0,pi]
# first find the vectors from q to p and q to r
v1 = np.array([p[0]-q[0],p[1]-q[1]])
v2 = np.array([r[0]-q[0],r[1]-q[1]])
if np.linalg.norm(v1) == 0 or np.linalg.norm(v2) == 0:
# if either vector is the zero vector, return pi
exception = "zero vector"
# print p,q,r
print("p is",p)
print("q is",q)
print("r is",r)
raise Exception(exception)
if np.dot(v1,v2)/(np.linalg.norm(v1)*np.linalg.norm(v2)) > 1 or np.dot(v1,v2)/(np.linalg.norm(v1)*np.linalg.norm(v2)) < -1:
exception = "arccos not defined"
# print p,q,r
print("p is",p)
print("q is",q)
print("r is",r)
print("v1.v2 is",np.dot(v1,v2))
print("norm v1 times norm v2 is ",np.linalg.norm(v1) * np.linalg.norm(v2))
raise Exception(exception)
# find the angle between the vectors
angle = np.arccos(np.dot(v1,v2)/(np.linalg.norm(v1)*np.linalg.norm(v2)))
return angle
def cosine_of_angle_at_point(p,q,r):
# given three points p,q,r, return the cosine of the angle at q
# angle is in radians, in [0,pi]
# first find the vectors from q to p and q to r
v1 = np.array([p[0]-q[0],p[1]-q[1]])
v2 = np.array([r[0]-q[0],r[1]-q[1]])
if np.linalg.norm(v1) == 0 or np.linalg.norm(v2) == 0:
# if either vector is the zero vector, return pi
exception = "zero vector"
# print p,q,r
print("p is",p)
print("q is",q)
print("r is",r)
raise Exception(exception)
# find the angle between the vectors
cos_angle = np.dot(v1,v2)/(np.linalg.norm(v1)*np.linalg.norm(v2))
if cos_angle > 1:
cos_angle = 1
if cos_angle < -1:
cos_angle = -1
return cos_angle
# debug: check that the angle at a point is between 0 and pi
# p = [1,2]
# q = [2,1]
# r = [1,1]
# print(angle_at_point(p,q,r))
# q: what would lead to an invalid argument error to arccos?
# a: if the dot product is greater than the product of the norms, then the
# angle is greater than pi/2, and the arccos function is not defined
def acute_triangle(p,q,r):
# given three points p,q,r, return True if the triangle is acute
# and False otherwise
# find the angle at each point
cos_angle_p = cosine_of_angle_at_point(q,p,r)
if cos_angle_p <= 0:
return False
cos_angle_q = cosine_of_angle_at_point(p,q,r)
if cos_angle_q <= 0:
return False
cos_angle_r = cosine_of_angle_at_point(p,r,q)
if cos_angle_r <= 0:
return False
return True
# given a list of points, and a candidate point, return True if the candidate
# point can be added to the list without forming an acute triangle
def can_add_point(point_list, candidate_point):
# check if the candidate point can be added to the list without forming
# an acute triangle
# first check if the candidate point is already in the list
if candidate_point in point_list:
return False
# check if the candidate point forms an acute triangle with any pair of
# points in the list
for (i,p) in enumerate(point_list):
for (j,q) in enumerate(point_list):
if i < j and p != q:
if acute_triangle(p,q,candidate_point):
return False
return True
# given a list of points, return the list of points that can be added to the
def points_that_can_be_added(point_list):
# given a list of points, return the list of points that can be added to
# the list without forming an acute triangle
# first generate the list of points that can be added
points_to_add = [p for p in all_points if can_add_point(point_list,p)]
return points_to_add
# given a starting list of pairs return inital list of pairs plus candidate for the pairs
def apply_symmetry(pair):
# given a pair of points, apply the symmetries of the square to the pair
# and return the list of pairs
# since the coordinates of the points are in [1,9], we can use the
# symmetries of the square to generate all possible pairs
# first generate the list of symmetries of the square
# 8 transformations: identity, 90 degree rotation, 180 degree rotation,
# 270 degree rotation, reflection across horizontal, reflection across
# vertical, reflection across diagonal, reflection across other diagonal
# identity
identity = pair
# 90 degree rotation
rotation_90 = [N + 1 - pair[1],pair[0]]
# 180 degree rotation
rotation_180 = [N + 1 - pair[0],N + 1 - pair[1]]
# 270 degree rotation
rotation_270 = [pair[1],N + 1 - pair[0]]
# reflection across horizontal
reflection_horizontal = [pair[0],N + 1 - pair[1]]
# reflection across vertical
reflection_vertical = [N + 1 - pair[0],pair[1]]
# reflection across diagonal
reflection_diagonal = [pair[1],pair[0]]
# reflection across other diagonal
reflection_other_diagonal = [N + 1 - pair[1],N + 1 - pair[0]]
# put all the transformations into a list
transformations = [identity,rotation_90,rotation_180,rotation_270,reflection_horizontal,reflection_vertical,reflection_diagonal,reflection_other_diagonal]
return transformations
# remove symmetric pairs from the list of pairs
def remove_symmetric_pairs(list_of_pairs):
# given a list of pairs, remove the symmetric pairs from the list
new_list_of_pairs = []
removed_pairs = []
for pair in list_of_pairs:
if pair not in removed_pairs:
new_list_of_pairs.append(pair)
pairs0 = apply_symmetry(pair[0])
pairs1 = apply_symmetry(pair[1])
for i in range(8):
if [pairs0[i],pairs1[i]] not in removed_pairs:
removed_pairs.append([pairs0[i],pairs1[i]])
if [pairs1[i],pairs0[i]] not in removed_pairs:
removed_pairs.append([pairs1[i],pairs0[i]])
print("checked",len(removed_pairs),"symmetric pairs")
print("new list of pairs has length",len(new_list_of_pairs))
# print("removed pairs are",removed_pairs)
# sort the new list of pairs
new_list_of_pairs = [sorted(item) for item in new_list_of_pairs]
return new_list_of_pairs
def starting_list(list_of_pairs):
# given a list of pairs, return the list of pairs plus the list of points
# that can be added to the list of pairs
starting_list = []
for pair in list_of_pairs:
candidate_points = points_that_can_be_added(pair)
starting_list.append((pair,candidate_points))
return starting_list
# given a list of points and a candidate list, reduce the candidate list to
# only those points that can be added to the list of points
def reduce_candidate_list(point_list, candidate_list):
# given a list of points and a candidate list, reduce the candidate list to
# only those points that can be added to the list of points
reduced_candidate_list = []
for candidate in candidate_list:
if can_add_point(point_list,candidate):
reduced_candidate_list.append(candidate)
return reduced_candidate_list
# function to remove symmetric lists from the queue
def remove_symmetric_lists(queue_lists, queue_candidates):
# given a queue of lists and a queue of candidates, remove the symmetric
# lists from the queue_lists and the corresponding candidates from the
# queue_candidates
new_queue_lists = []
new_queue_candidates = []
removed_lists = []
for i in range(len(queue_lists)):
if queue_lists[i] not in removed_lists:
new_queue_lists.append(queue_lists[i])
new_queue_candidates.append(queue_candidates[i])
# lists should be sorted no need to check for permutations
# any duplicates should by above if statement
# symmetry_list will be a list of lists of pairs
# there will be 8 lists of pairs
# initialise to 8 empty lists
symmetry_lists = [[] for i in range(8)]
for pair in queue_lists[i]:
current_list = apply_symmetry(pair)
for k in range(8):
symmetry_lists[k].append(current_list[k])
symmetry_lists = [sorted(item) for item in symmetry_lists]
# for each list in symmetry_lists, check if it is in queue_lists,
# possibly in a different order, and if so, "remove" it from the
# queue_lists by adding it to the removed_lists list
for list in symmetry_lists:
removed_lists.append(list)
return new_queue_lists, new_queue_candidates
def remove_non_likely_lists(queue_lists, queue_candidates, longest_length):
# given the queue of lists and the queue of candidates, remove the lists
# that are not likely to be longer than the longest list
# if length of list plus length of candidates is less than or equal to
# length of longest_length, then remove the list from the queue
new_queue_lists = []
new_queue_candidates = []
for i in range(len(queue_lists)):
if len(queue_lists[i]) + len(queue_candidates[i]) > longest_length:
new_queue_lists.append(queue_lists[i])
new_queue_candidates.append(queue_candidates[i])
return new_queue_lists, new_queue_candidates
# idea to make a big queue out of the starting list, then pop off the first
# element, add the candidate points to the list, and add the new list to the
# queue
# kind of a depth first search
def main():
# method 1 is kind of slow:
# append to start of list should explore a possible position to the end
# before exploring the next possible position
# allows to prune the search tree more effectively
# make a queue out of the starting list
reduced_pairs = remove_symmetric_pairs(all_pairs)
#queue = starting_list(all_pairs)
queue = starting_list(reduced_pairs)
# loop through the queue and keep track of the longest list
longest_list = []
counter = 0
while len(queue) > 0:
# pop off the first element of the queue
current_list = queue.pop(0)
if len(current_list[0]) + len(current_list[1]) > len(longest_list):
# add the candidate points to the list
new_lists = []
new_candidates = []
for candidate in current_list[1]:
new_list = current_list[0] + [candidate]
# reduce the candidate list
reduced_candidate_list = reduce_candidate_list(new_list,current_list[1])
if len(reduced_candidate_list) == 0:
# we have reached a dead end, so check if the new list is longer
# than the longest list
if len(new_list) > len(longest_list):
longest_list = new_list
print("longest list so far has length",len(longest_list))
print("longest list so far is",longest_list)
else:
# add the new list to the queue
# queue.append([new_list,reduced_candidate_list])
# append to start of list
if len(reduced_candidate_list) + len(new_list) > len(longest_list):
# if the length of the reduced candidate list plus the length
# of the new list is less than or equal to the length of the
# longest list, then we don't need to add the new list to the
# queue
new_lists.append(sorted(new_list))
new_candidates.append(reduced_candidate_list)
# throw away symmetric pairs in new_lists and new_candidates
new_lists, new_candidates = remove_symmetric_lists(new_lists, new_candidates)
for i in range(len(new_lists)):
queue.insert(0,[sorted(new_lists[i]),new_candidates[i]])
counter += 1
if counter % 1000 == 0:
print("counter is",counter)
print("length of queue is",len(queue))
print("length of longest list is",len(longest_list))
print("longest list is",longest_list)
# prune the queue by removing symmetric sets
# print("length of queue is",len(queue))
# queue_pairs , queue_candidates = remove_symmetric_lists([item[0] for item in queue],[item[1] for item in queue])
# queue_pairs, queue_candidates = remove_non_likely_lists(queue_pairs, queue_candidates, len(longest_list))
# queue = [(queue_pairs[i],queue_candidates[i]) for i in range(len(queue_pairs))]
# print("length of pruned queue is",len(queue))
longest_list = sorted(longest_list)
print("longest list has length",len(longest_list))
print("longest list is",longest_list)
# main 2 is like a breadth first search
def main2():
# method 2 to try to speed up the search:
# append to end of list should explore all possible positions of a given
# length before exploring the next length
# This is slower than method 1 probably because the search tree is not
# pruned as effectively
# Try to prune the search tree by removing symmetric pairs
# make a queue out of the starting list
reduced_pairs = remove_symmetric_pairs(all_pairs)
#queue = starting_list(all_pairs)
queue = starting_list(reduced_pairs)
# split the queue into two lists: one has the pairs of stones, the other the candidates
queue_pairs = [sorted(item[0]) for item in queue]
queue_candidates = [item[1] for item in queue]
depth = 2
longest_length = 0
longest_list = []
# loop through the queue and keep track of the longest list
# append to the end of the queue, and when the depth is increased,
# prune the queue by removing symmetric sets
while len(queue_pairs) > 0:
if len(queue_pairs[0])> depth:
# we have reached the end of the queue, so increase the depth
depth += 1
print("increasing depth to",depth)
print("length of queue is",len(queue_pairs))
# prune the queue by removing symmetric sets
queue_pairs, queue_candidates = remove_symmetric_lists(queue_pairs, queue_candidates)
queue_pairs, queue_candidates = remove_non_likely_lists(queue_pairs, queue_candidates, longest_length)
print("length of pruned queue is",len(queue_pairs))
# pop off the first element of the queue
current_list = queue_pairs.pop(0)
current_candidates = queue_candidates.pop(0)
if len(current_list) > longest_length:
longest_length = len(current_list)
longest_list = current_list
print("longest list so far has length",len(longest_list))
print("longest list so far is",longest_list)
for candidate in current_candidates:
new_list = current_list + [candidate]
# reduce the candidate list
reduced_candidate_list = reduce_candidate_list(new_list,current_candidates)
if len(reduced_candidate_list) == 0:
# we have reached a dead end, so check if the new list is longer
# than the longest list
if len(new_list) > len(longest_list):
longest_list = new_list
print("longest list so far has length",len(longest_list))
print("longest list so far is",longest_list)
else:
# add the new list to the queue
# queue.append([new_list,reduced_candidate_list])
# append to end of list
queue_pairs.append(sorted(new_list))
queue_candidates.append(reduced_candidate_list)
longest_list = sorted(longest_list)
print("longest list has length",len(longest_list))
print("longest list is",longest_list)
main()
# main2()
main() is kind of the depth first search because I have a queue where it keeps appending deeper and deeper lists to the start, like positions with more stones, then it’ll finish one branch and move onto others probably ![]()
main2() does a kind of breadth first one in the sense it takes all 2 stone sets, makes the three stone ones, then takes those and makes the four stone ones and so on.
I tried to prune away positions that are symmetric, by usuing symmetries of the square and pruning positions where the number of candidates to be added couldn’t be larger than the current largest found.
In addition to pruning symmetries, there is probably a lot to be pruned from just finding one triangle. You can basically skip all the combos between when the triangle is “formed” and the triangle is “broken”.
For example:
There is an acute triangle in the top left corner (marked with triangles):
It doesnt matter where the 20th stone is (marked with square), there will always be the same triangle in the corner. Skip 60 intermediate positions until the triangle is broken:
The benefits are more pronounced when there are more stones “after” the triangle. Like this board, the number of combinations we can skip is C(61, 17) ~= 5e14
Skips to:
By the way, if the squared side lengths are A, B, C, where A corresponds to the longest side. Then, the triangle is acute if and only if A < B + C.
This should be a bit faster to compute, and everything is via simple integer operations, avoiding concern about numerical precision causing potential issues.
I’m not sure exactly what you mean, but the way I was doing it was I started out with two stone pairs, then generated only combinations/candidates that didn’t produce an acute triangle with those pairs. Then each time I choose - candidate to add, I reduce the old list of candidates by throwing away ones that don’t work with the updated list.
Is that kind of what you mean? It wasn’t arbitrary checking all combinations, there was a lot of filtering to begin with ![]()
The depth first search could find and 18 very quickly that way but the 19 took a good bit longer.
That does sound interesting, maybe I’ll play around with that so ![]()
Ohh I see I didn’t quite understand how the search worked. That sounds better than what i was thinking. Thanks for explaining!
Symmetric version of the 19-stone solution:
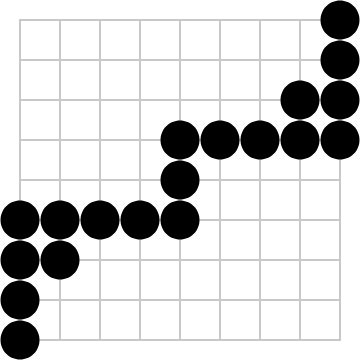
Similar solution for the 19*19 board:
For board sizes N = 2, 3, 4, we can’t do better than 2N stones (which can be achieved by filling two columns).
N = 5 is the smallest board where we can squeeze in two B2 bombers, which achieves a total of 2N+1 stones:

For all N > 5, we can achieve 2N + 1 by placing two B2 bombers in the lower left and then extending this staircase as far as we like:
So the exciting open question is, is it possible to do better than 2N + 1 stones on any board size N?
My initial intuition was that with more wiggle room on the larger boards we should be able to fit more extra stones along this diagonal, but after playing around with it a bit I’m not so sure.
For this family of solutions, we have a lot of freedom with where we place the bombers and how the path goes between them. But the path must stay between these borders created by the bombers:
Another way of looking at it is that we can start with any path going between the corners. After that there will be at most two places left where we can add stones, corresponding to the maximum deviations of the path in both directions:
If anyone else wants to play around with it (maybe to try to find some solutions that are not based on this same path idea?) I made this tool to check my solutions.
You can click/drag to place stones and press space to toggle the display of “forbidden” intersections. Increase/decrease board size with up and down arrow keys.
So these are direct paths in a sense that say moving from bottom left to top right the either the row or column is always increasing? No backtracking.
That’s very interesting, the tool looks fun to play with as well! I’ll have to try it out ![]()
Right, forgot to clarify that! Such a path will never contain any acute triangles, and will always consist of exactly 2N - 1 stones, so that path plus the two extra stones that can be fit in for N > 4 gives the 2N + 1 lower bound.
I still find this kind of mad, believable but mad ![]() Is it coming from the right angles in the grid itself? Is there’s a nice proof of it?
Is it coming from the right angles in the grid itself? Is there’s a nice proof of it?