In category theory a dual of a category is done by reversing the direction of all the arrows/morphisms. Naturally any duality that is constructed with the category theory definition would have the property that the dual of the dual is the original as reversing the arrows twice creates the original category.
1 Like
Let’s take Wikipedia:
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often (but not always) by means of an involution operation.
Then, moving on to the page about involutions:
In mathematics, an involution, or an involutory function, is a function f that is its own inverse.
I must admit that Wikipedia mentions it being often, and not always, an involution, but from my experience this is rather rare.
Well, my drawing is not self-dual, I think that’s what I was trying to show in a way 
I’m not sure, it helps make other things more clear, but as for counting in Go, I’m not so certain about applicability of pure mathematics.
Of course, stretching out is not so much what we do, but we do move stones inside territory to get to a different position that’s easier to count (usually rectangles). In a way you could interpret this as keeping the board the same but moving the location of the empty intersections / vertices. Mathematically (or rather, topologically) this doesn’t change much about the graph, though.
As in, we’d interpret moving the white stone in this board, not as moving the white stone, but as moving the underlying structure of the board:
like this:
1 Like
In actual counting after end-game, rearranging to easier counting blocks like squares and certain shapes are pretty common. But usually required moving pieces pretty far into different territory and fill in the smaller one first. Are there equivalent as you said moving the graphs? The purpose of the rearranging is to make it easier to tell on a glance, and strait boarder would make them easy to verify not just visualize.
And sometimes people do cheat with moving stones slightly to shape easy to count but not equivalent to the end-game. Would say a connected graph help with prevent that and say only allow certain swap?
My dearest yeb,
Please, please allow us to take a little space here and continue discussion. We promise not to deviate much. More eyeballs on the thread make it popular, which is a good thing to the original question. Moreover, during this trying Covid time, it’s harder for people to have face-to-face conversations. So it might be good to take every chance to start a topic, communicate, and meet human’s social needs. I see some people enjoying it. Please don’t disappoint them.
English is my 4th language and I had to look up in a dictionary to know the meaning of those words. But I don’t see pretentious language, or feel condescended; because they look perfectly natural in the sentence. Same for math. If you focus on truth first and others feelings second, nothing is pretentious and no one should feel condescended.
Sorry maybe I have jumped too many steps, but I believe those concepts are closely related. You have to forgive me, for we read ahead in the game of Go.
Sincerely,
A Humble Go Player
2 Likes
Could you please explain how it is ultimately related to the optimization theory concept of duality?
This is what I mean by condescending, when you imply that I can’t follow the steps or read ahead.
1 Like
Our bias for intersections is simply because of our familiarity with using them in Go. But one major issue is that a 19x19 board defines 18x18 small rectangles. So you need a 20x20 board to play a 19x19 game on small rectangles. (Note that the small rectangles are not squares since a Go board is not square.)
2 Likes
Hey, I never thought of playing inside a grid would make the secret of none-square square grid reveals to the world. 
(quick squeeze them back to squares)
1 Like
It’s even worse: the stones don’t even fit, since they are (supposed to be) very slightly too wide.
1 Like
In Go, the thing we’re interested in is how many empty intersections there are. When the endgame has concluded, all intersections form a 5-coloured graph: (1) those intersections having a white stone, (2) those intersections having a black stone, (3) those intersections belonging to white territory, (4) those belonging to black territory, and (5) those belonging to neither (dame & seki). We’re only interested in the total number of intersections that are empty and belong to either white or black (so options 3 & 4).
Removing the other nodes doesn’t change the number of nodes of type 3 or 4, so we get a graph like this:
Let’s say we count white-owned intersections. Moving intersections around does not change the number of white intersections: we’re only moving things around. So the number of white intersections is, what is called, invariant under the mathematical operation of moving it around:
For all our purposes, we may as well try to count this graph:
That’s what I was doing in my second diagram above, changing the location of the intersection, without changing which intersection it was.
Of course, swapping two vertices around or swapping the colour of the two vertices also does not change the total number of vertices of a single colour. This is what we do in normal counting on a real board: we change the colour of an empty white-owned intersection to an intersection with a white stone, and the original intersection that had the white stone is changed to an empty white-owned intersection. Again, the number of vertices of any certain colour is invariant under this operation.
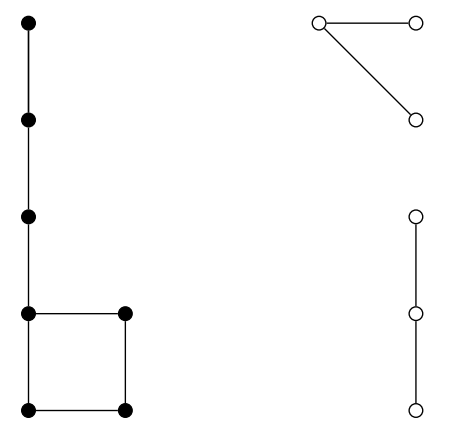
However, as graphs, it does depend how you present this. The following two graphs are not considered equivalent for anyone studying graphs, while they are of course equivalent as far as Go is concerned:
For example, the left graph has three connected components, and the right one has two.
Neither is the following for someone studying coloured graphs, since in the above graphs each component only contains similarly coloured vertices, while here we have both black and white vertices in the same component. However, the underlying structure of the graph is the same, so if you don’t care about colouring, the graphs are equivalent.
Then you can think about how you present the graph. Somebody who sees the length of the edges in the graphs to have an importance wouldn’t mind moving points around like this:
but would mind if you move points like this:
Somebody who only considers the way a graph is embedded into the plane may find the above two graphs equivalent, but find them different to the one below, since there is no way to move the white dots into the square without having to cross one of the black edges:
And so on, it really depends what your purpose is
3 Likes
I don’t think it would be possible to make the stones slightly too wide to fit into the “squares” without also making them slightly too wide not to bump into each other when placed on adjacent intersections…?
Exactly. Go try it out on your go board and you’ll be in for a surprise 
I don’t have a go board, but I feel you must have misread my post. I’m saying if it were true that the stones are too wide to fit into the squares, they must also be too wide not to bump into each other when placed on adjacent intersections, which they clearly aren’t.
Yes, I did read your post correctly: they actually are too wide and bump into each other when placed on adjacent intersections, or at least that’s what they are supposed to be (or at least, for the Japanese biconvex go stones, not so sure about the Chinese-style stones).
Another interesting thing is that the black stones are slightly larger, to make them appear equal in size on the go board as the white stones.
4 Likes
scratches head in confusion If they were so wide that they’d bump into each other, it would be almost impossible to play a game with 300+ moves, wouldn’t it…?
1 Like
It’s only very slight, here’s a picture of my go board & stones, including close-up to show the black row slightly overshoots:
See also this Senseis page
7 Likes
In a normal game, a “line up” especially black stones would slightly offset like a zig-zag wave (since the length is longer than the width in a grid, there is room for that). And it’s very rare with a strait stick all the way across the board in real game with all black stones.
3 Likes
Fascinating, thanks for the pictures!!
So actually your white stones are smaller than grid, while black stones are slightly bigger.
I don’t have a proper goban and stones but I always thought that all stones were slightly bigger.
1 Like
Yes, so did I, I was a bit surprised to find out white is smaller 
2 Likes
I think for the idea of duality not always being an involution, in some cases it might boil down to equality vs isomorphic. In the case of finite dimensional vector spaces, the dual of the dual of a vector space is only isomorphic to the original space. I believe this is an example of why one wouldn’t think of this mapping from a space to it’s dual as being an involution (in say the category of vector spaces). It’s probably the case for graphs as well when one looks at the dual of the dual, unless one has some rigid idea of what the vertex sets are, then the dual of the dual might only be isomorphic.
2 Likes