Diplomatic Go

Go Variants
203

Am I correct that we have the following proposals for player incentives? Am I missing any?

  • The goal is to win the game, either solely, or as a member of a draw. Players who don’t win automatically lose. No method of losing is preferable according to the rules, players should make their own goal in this scenario.
  • The goal is to maximise your score, which is your total area (Tromp-Taylor) at the end of the game. Players can fight to place second, third, etc. Players who cannot improve their position should make their own goal in this scenario
  • The goal is to maximise your score. Points can be earned by cashing out, which locks your score in place and bars you from playing any further moves. Under discussion is exactly what this score depends on (stones on the board, remaining players, number of rounds so far, etc)
  • The goal is to maximise your score. Points can be earned from a fixed pool by cashing out. Each time a player cashes out, all players get rewarded the number of points of area they own on the board, even when eliminated. After all players have cashed out, the remaining points in the pool get distributed proportionally to the remaining areas on the board.
  • The goal is to be part of an alliance that controls the majority of the board and to maximise your score. Points can only be earned at the end of the game if you are part of an alliance controlling the majority of the board, and is proportional to your own area.
6 Likes
204

In my latest proposal, you may gain points even after dropping out, as long as your stones are left on the board. After thinking through some example cases, I came to the conclusion that this variation is more well-behaved.

(Also note that in that proposal, everybody with stones on the board gets paid in each payout.)

4 Likes
205

While I ultimately prefer the first option, I think we should try something different. Out of the rest, I prefer the second one the most, since it is conceptually simpler and does not encourage people to stop submitting moves early.

I think the last option makes for a very different game. Having the most points does not necessarily mean winning, and it seems like it would be incredibly hard to achieve a solo win, since anyone approaching a majority could probably be immediately stopped by everyone else forming an alliance. Such a game would revolve heavily around negotiating alliances and end game considerations.

206

Could someone give me a brushup on the whole ruleset, please?

Seems like some information is being implicitly carried over from earlier in the discussion, which is fine; I’d just like to know exactly what the rules are.

eg. how many move choices do we get, for use in the event of collisions (which I assume still result in no move on that point for either player)?

1 Like
207

The exact rules are described in the first post. The thing that’s not yet decided is how points are earned, but apart from that, I’m planning on keeping every other aspect of the rules.

4 Likes
208

I’d like to make some slight adjustments to my last proposal.

  1. I don’t think we need the old elimination mechanic anymore, the dropout mechanic can replace it. It would be very hard to “forcibly” eliminate a player on the larger board anyways, and the rules become simpler without it.
  2. Without the elimination mechanic, I would once again move the payout to before moves are resolved in a given round. This makes it so that when you drop out, you are agreeing to be paid for the board as you see it, rather than the board after all the other players move, and some of your stones may have been removed. (The main reason I moved the payout to after the moves in the last proposal was to make it fit better together with eliminations)
  3. I think each payout should be made in the same way, by dividing a fixed amount according to the proportion of the total score each player has. This avoids having two different types of payouts, and will also lead to more fine-grained differences to consider for players dropping out early (not only how many stones you have matters, but also how many stones the other players have), which leads to less choices without meaning.

For the last change, let me adress two “drawbacks”:

  • Doesn’t that make it harder to calculate your payout when dropping out?

Yes kind, but since you’re agreeing to the board as you see it, we could automatically calculate the potential payout and give that information as part of each new board.

  • Doesn’t this give too little importance to the final board position?

I don’t think so. Creating alive groups which stay on the board until the end is still the best way to profit. If we wanted to make the final board even more important, we could just add another (possibly larger) payout after everyone has dropped out, but that’s slightly less elegant and probably not necessary.

To sum up my new proposal: At any time a player can drop out instead of submitting a move. Every time some player drops out, every player gets paid according to how big their score is compared to the total score.

Instead of voting for resign/draw, at any time a player can publicly suggest how to distribute the remaining prize pool. If every player agrees (except those that have already dropped out and also have no stones on the board) the game can be ended directly. This is just a shortcut to avoid having to remove dead stones from the board if the outcome is obvious.

It’s completely fine to not worry about the finer details of the payouts. If you just play “normally” and try to stay alive with your stones, you will be rewarded for that. The precise definition of which outcome to prefer is only there if you really want something like that, noone is forcing you to care about it, and noone should fault you for playing “suboptimally” from their point of view.

If you prefer the notions of losing/drawing/winning to that of a payout, I would look at it like this:

Imagine each player has contributed an equal amount to make the prize pool. Walking away with exactly the same amount would be the equivalent of a draw for you personally, a completely even result. Anything less than that is a “loss”, just with some added granularity on how big the loss is. Likewise, anything more is a “win”, but some wins are bigger than others.

You are also free to aim for making more money than any other player in this particular game if you wish, but I would recommend that you instead think in terms of making more money than anyone else “in the long run”. It’s up to each player though.

4 Likes
209

I have concerns about the consequences of not having an elimination mechanic. What if people simply refuse to drop out, even if they have no stones on board? As you pointed out in a different thread, making a 100% alive group is increasingly difficult with many players. If all players refuse to “cash out”, it seems possible to me that no player may ever be able to create a group that is able to permanently stay on board. With repeated captures the game may only end when there is a repetition.

Edit: Except for this criticism I think it sounds very good.

210

There’s a lot to digest there, so I will have to consider it all more carefully, and I will most likely have more to say, but I just want to express (and now second @martin3141’s response, which wound up making the same point while I was typing this out) that a lack of elimination mechanic could allow a player to continue placing stones until their very bitter end of the game, in order to continue influencing the outcome. This would have life/death implications for the remaining players, and a player with no stones left on the board, could even come back to life by eventually getting space to establish a living group after helping to wipe out another player’s group.

1 Like
211

It’s a valid concern, but I don’t think the old elimination mechanic does much to help prevent this scenario. As long as the board is not completely filled up, it’s so easy to play stones wherever to stay in the game.

Basically, if we have to count on all players being forcibly eliminated to stop affecting the game, that’s no good anyways.

Maybe we will have to reevaluate after looking at some examples, I’m open to keeping the elimination mechanic if others prefer, I just wanted to make my proposal without it. (it’s easy to put it back in as a forced drop-out when you no longer have any stones on the board)

2 Likes
212

Yes it is fairly difficult to forcibly eliminate another player, but it’s not out of the question if people cooperate in order to do so. For example in the last game, I was proposing Vsotvep and Haze to work together towards capturing your group, le_4TC (because I thought that was my best strategy). Vsotvep told me he was concerned that you would be able to create a new group subsequent to the capture, and that players would continue teaming up to take out the groups of the advantageous players. I thought about this, and in the last game, I believe we could have avoided this with ample preparation, by filling the inside territories and dame until all empty intersecions are isolated.

213

Yeah, the issue is that it was difficult on 9x9, and just gets harder and harder the bigger the board is.

1 Like
214

Then how about modifying the elimination criterium a bit? Here are two ideas I just had:

1.) A player is eliminated if they have 0 stones on board or if they have exactly 1 stone on board, and this stone was placed last round (only effective after a fixed number of rounds).

2.) Every round a player must secretly choose one of their chains as their “main chain” and tell the arbiter. If the main chain of a player is captured, they are eliminated. If a player doesn’t choose a chain (for whatever reason), per default their chain with the most liberties is chosen, and if there are multiple, the one which most recently had a stone added is chosen (this may be a bit tedious to check, but it shouldn’t come up too often). (also only effective after a fixed number of rounds)

The second one somehow creates a fun sub-game where players whose “main group” is about to get captured could choose one of their stray stones to stay in the game, even if that stone is vulnerable to capture too.

215

I’ll try to illustrate my proposal in practice using the first game. Assume each player has paid $100 to take part in the game, so there is a total prize-pool of $500, and each payout will distribute $100.

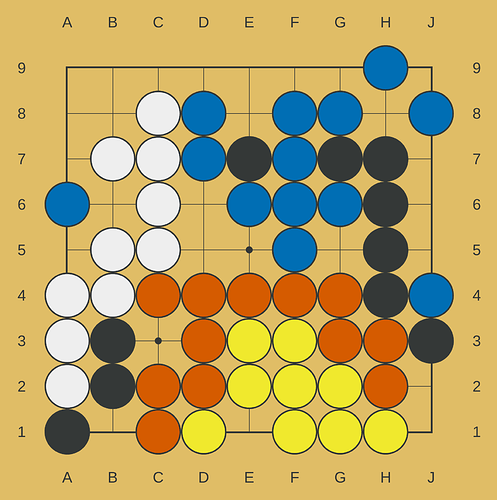
image
In this position, yellow might expect to be captured in the coming round, so decides to drop out now. The fact that yellow has dropped out is announced together with the other moves from the next round, but the dropout is handled first.

In “unsettled” positions, you mostly get rewarded for how many stones you have on the board; the only intersections that count as territory in this case are E1 and J9. Taking those into account, we get the following areas:

Blue: 14
Red: 12
White: 10
Black: 10
Yellow: 10

The total amount of claimed area is 14 + 12 + 10 + 10 + 10 = 56.

Yellow, black and white will thus all get $100 * (10 / 56) ≈ $17.86, while red gets $21.43 and blue gets $25.00.

Now let’s jump ahead to this point (where the real game ended):
image
Black should maybe have dropped out earlier (right before their group on the right was captured), but let’s assume they decided to stay in the game until this point. It looks very likely that the top group will be captured on the next move, so they drop out now, and another payout is made.

Areas
Red: 28
White: 23
Blue: 22
Black: 6
Total: 79

Money (old + new)
Red: $21.43 + $35.44 = $56.87
White: $17.86 + $29.11 = $46.97
Blue: $25.00 + $27.85 = $52.85
Black: $17.86 + $7.59 = $25.45
Yellow: $17.86 + $0 = $17.86

Notice that since all yellow stones have been captured before this, yellow will not gain any more money during the rest of the game.

In the coming moves, the black chain will be captured, and that area will be divided between white and blue. Red might also try to throw a stone or two in there, which may or may not survive until the dropout depending on the exact sequence. For simplicity, let’s assume we reach this position:

image
image783×784 50 KB

Here white drops out, since blue and red will probably capture on the next move. White could try to play A8 first, but if blue and red foresee this, they could work around it with a planned collision. The two extra points are probably not worth the big risk for white.

Areas
Red: 28
White: 26
Blue: 25
Black: 1
Total: 80

Money (old + new)
Red: $56.87 + $35.00 = $91.87
White: $46.97 + $32.50 = $79.47
Blue: $52.85 + $31.25 = $84.10
Black: $25.45 + $1.25 = $26.70

Next up, white is captured. Blue and red divide the area, each trying to claim as much as possible. Let’s assume that the final board looks something like this:

image
image780×778 40.9 KB

Both players drop out in this position. They could try throwing in stones into the others territory and then immediately dropping out, but if both do this and then only one of them drops out, the other one is at an advantage (they will empty their own territory before dropping out). Assume for simplicity that they both decide that this is the best that they can do. Since both drop out here, we get a “double” payout from this position.

Areas
Red: 40
Blue: 41

Money (old + new)
Red: $91.87 + $49.38 + $49.38 = $190.63
Blue: $84.10 + $50.62 + $50.62 = $185.34

Payout summary
Red: $190.63
Blue: $185.34
White: $79.47
Black: $26.70
Yellow: $17.86

Even with the doubled importance of the final position, blue didn’t quite catch up in terms of money, since they only barely catched up in terms of area. If blue had managed to get 43 points in the final position, that would have been enough to make more money than red in total.

Personally, since I think we shouldn’t think in terms of “winning” an isolated game, but rather in terms of maximizing expected winnings, I don’t mind the fact that the “winner” in the final position isn’t also the one making the most money. But if other people don’t like this, we could make such situations much rarer by doing an extra (bigger) payout right at the end, like I’ve mentioned before.

4 Likes
216

A third option:

3.) If after x rounds, you have less than x/2 stones on the board, you’re eliminated.

Of course the fine details of the relationship between rounds and stones can be adjusted, but I think something like this could work quite well. I might look at some examples later (unless someone else does it first), but right now I need a break after writing that last post :stuck_out_tongue:

4 Likes
217

imageimage
On the left board, 13 moves have been made in total, and each player has more than 13/2 = 6.5 stones on the board, so noone is eliminated. After the next move, yellow is eliminated since they have fewer than 14/2 = 7 stones.

Black would stay in the game up until this point:
imageimage
On the left, 19 moves have been made, and black has 10 stones on the board. Black is eliminated after the capture on the right.

In the final position of the first game, 32 moves have been made:
image
All of the remaining players have at least 16 stones, so noone is eliminated yet.

With this elimination rule, we could actually restate the objective of the game as “be the last player standing” (think about what happens after the board is filled with immortal groups). I find this quite elegant, and I’m guessing people might prefer this to a payout system.

6 Likes
218

I really like this elimination rule. It’s a lot more elegant than the payout system and it actively encourages weak players to kill other players, to get enough space to not be eliminated.

6 Likes
219

I like this proposal. It essentially goes back to a “winner takes all” paradigm, which I like. The goal is to be the last person eliminated (or part of the last group to be eliminated, which is essentially a draw). It also puts a more urgent deadline on how long a game could possibly last, which is nice for scheduling purposes, and obviates the need for addressing cycles. I think players should still be able to vote for a draw and/or resign (in order to either realize interesting endgame threats, or to speed up the game when the outcome seems inevitable).

An interesting complication is that players are forced to shore up eye space and clean up the dead stones left behind by the rivals that they are aiming to outlast. I think you mechanism design highlights your desire to make it easier to eliminate pesky rivals. :wink:

I support using this objective over the alternatives for the second game.

2 Likes
220

Yeah, it should always be possible to end the game earlier when everyone agrees that the outcome is obvious. I would also support having the option to resign individually, i. e. drop out early if you have no interest in continuing the game.

(Ideally I think everyone should aim to stay in the game as long as possible, even if they think they have no chance to win. But if someone doesn’t care much, I think they should have the option to resign.)

221

Is this anything different than a player simply choosing to submit a standing order to pass and a standing vote to resign and accept any draw?

I think it’s important to distinguish between players that may wish to “resign” like that versus simply lacking the time/interest to continue playing (even though they may still have a viable position). In the latter case, I think it would be better to find a replacement player to avoid disrupting the game, like how I replaced @HHG with @martin3141 in the first game. I think the alternative of resigning by standing pass must always be made by the player, since it’s difficult for the arbiter to step in and make such a judgement to do so.

If someone is not going to care much about the game, they should consider whether they join in the first place. A game becomes much less interesting when not all of the participants are really engaged in it.

3 Likes
222

Yes, I meant that the referee will publicly announce that the player has resigned and will no longer be making moves.

If a player just loses interest for personal reasons, then finding a replacement is of course nice. If they lose interest due to thinking the position is hopeless for them, I was thinking maybe letting them resign was the best option. But if we can get everyone onboard with “just try to stay in as long as possible”, (meaning that even if you will be the first eliminated player, staying on the board a few extra moves is preferable) then an individual resign option wouldn’t be necessary.

1 Like