In this color flip(white black)the resualt color did not change.
I am just saying.
Interesting … let me give you an example where this does not apply.
This Koan knows Buddha-Nature:

This Koan does not:

We should really come up with a rule that explains this subset of koans, at least:










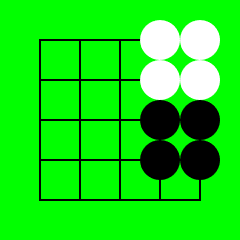

In them both have five liberties.
So the length does matter too.
“The white chain needs to have equal or more liberties than the black chain, unless they touch in some specific way.”
Since I’m once again stuck, I’ll ask another question about the general form of the rule:
Could the rule immediately be generalized to an arbitrary graph?
Basically, does it only use properties like sizes of chains, which chains are connected to which, etc, without making any reference to lines/diagonals on the board (things which can’t necessarily be defined for arbitary graphs)?
Answer
Yes, the rule is invariant to the drawing of the graph.
What does that mean?
Think of a graph as points and lines connecting those points (in our case the grid on the go board). However, two different drawings of points and lines can describe the same graph.
Basically the graph is only the information how many points exist and how these points are connected to each other, but a graph doesn’t have to be drawn in a specific way. I hope this is a good explanation ^^
For example, here are two different (poorly-made) drawings of the same graph: 
For instance, if we were to place some black and white stones on the intersections in this picture:

Martin could tell us if it is red or green. This would not be possible if the rule were “each line contains the same number of white stones”, since lines only exist on our representation of the square board, not as a general property about graphs.
Okay, I see. What does that mean, the rule can be generalized into an arbitrary graph? What does arbitrary mean here?
Ah! But here, a point is only connected to three other points, and not to four like on the Goban. So that means … I don’t know, but it has an implication about the property of chains and liberties.
Yes, it’s a very different board, but you can still define “chains” and “liberties” in exactly the same way, so if the rule is for instance “every black chain has exactly three liberties” that would still work 
The rules of go, including concepts such as connectivity, chains, liberties etc. are based on the structure of the grid and not the drawing of the grid. Also the rules still work when applied to a different base graph, so one could play go on arbitrary graphs.
In the past I’ve made a go board featuring a different base graph:
Awesome choice of graph, I love that tiling 
Is the fun with this board still about the playing of the game or just about the process of designing and crafting?
Thank you, I had a lot of fun playing on this and recommend trying it sometime, if you have the chance 
Both are fun!
