Hehe. Okay, I think I’m starting to understand.
Somehow I didn’t answer the whole question, so:
show
The rule can be applied to any graph.
Here’s an app which let’s you play on some funky graphs, perhaps the images on that page also serve as some good examples of what is possible: http://www.lewcid.com/lg/lc/freedgo.html
(the above also links to this page http://www.di.fc.ul.pt/~jpn/gv/boards.htm which among other graphs contains the one Martin made above (well a slightly larger version to be specific, but based on the same tiling))
And to make this poor linguist here understand completely: The rule does not use the words or concepts of line, corner, center, edge, angle, diagonal, orthogonal. But it does use the concepts of more stones, fewer stones, liberties, chains, connection.
Very well put, that’s exactly right!
(unsurprisingly the linguist is better than the mathematician at putting things into words  )
)
I have a “Virgin STEM student vs. Chad Philologist”-meme somewhere in my database …
That means every guess with “within a 2x2 grid…” and “if white is further away from the edge …” and so on is wrong.
This means that the Rule is rather simple (-ish). I wish it were just “there are more white chains than black chains” or “the number of white chains is equal or more to the number of black chains, but only if the white chains have more liberties”
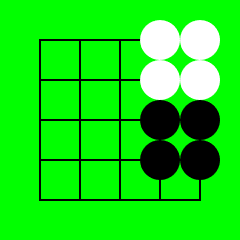
This one seems problematic for it to be something about white having more liberties.
The hane ones are very confusing to me. It would’ve made me think about white either having more groups or more liberties as in

but then the double hane would make even less sense

Yes, that’s exactly where I have trouble, too.
Basically yes, but if I wanted to be mean I could talk about cyclic subgraphs of length 4, which are precisely the 2x2-grids on a square board, but are also meaningful on arbitrary graphs. Distance between two nodes in a graph can easily be defined in general as the minimum number of “steps” you need to take between connected nodes to get from one to the other. However the concept of some nodes being on the “edge” of the graph is definitely not meaninful on arbitrary graphs, so yes, “distance to the edge” is ruled out. “Distance to a node with fewer than four connections” would be possible, but Martin wouldn’t be that misleading.
I’m probably just confusing things and you should ignore the above nonsense ^^ I just wanted to state for the record that we can’t rule out too much just by knowing that the rule works for arbitrary graphs: there is still a lot that can be defined on arbitrary graphs. But combined with the knowledge that the rule is reasonably simple, we don’t have to worry to much about this stuff.
All I really wanted to do with my original question was to rule out any sort of looking at whole lines or diagonals at once.
And this.


Strange.
I fell like there’s a strong connection to these here
Maybe we can list out some things it’s definitely not:
-
White has more groups

-
White has more liberties (total or otherwise), - or this one - If white is in contact then they have more liberties.

-
White has more groups and more liberties (total or even comparing groups of the same size)

-
White needs to be in contact with Black

-
If white is in contact with Black then white has at least as many groups (woops this one)

-
If the groups are in contact then they (or one of the groups) must be on the edge of the board

The rule does not refer to any complicated graph theory related concepts.
If you would like me to come up with such a rule, just tell me next game! 
I think it’s obvious that we’re having enough trouble with very basic concepts 
Also: If there are black stones present, there must be white stones present too. No green koan so far is all-black.
It depends on whether you want to possible make the game possibly inaccesible to more people. On the other hand, some people could actually find equivalent rules but in different language potentially unrelated to graph theory, and that would be interesting.
Don’t worry, I was joking of course 
I’m imagining simple rules that could work on other graphs too that it isn’t:
There is a non-self intersecting path through empty points of the board that passes though all of the groups liberties. It doesn’t work because


Maybe it inspires something else though.
An abstraction of this

is this:
 (if it were a legal Go position)
(if it were a legal Go position)
I’ve added the confirmed structural properties to the post with all the koans, for your convenience. Let me know if I forgot something.
If this was a legal board position, it would be red. Note that in the future I may take the liberty of not answering boards like this (where a chain has zero liberties), for that may (or may not) reveal too much about my rule. Who knows - maybe there are “illegal” board positions where my rule cannot be applied … ?

