Note: the post you’re about to read has been written with the intent to be understandable for people who have no background in mathematics. I apologize if this may result in a slower or more boring experience for the more mathematically adept as a result.
So I’ve been nerd-sniped.
Someone in chat asked “is there a Go equivalent to the Knight’s Tour problem?” and while we were pondering that, someone else came up with this: what’s the largest possible capture in a “normal” game of Go?
To be clear, by “normal” they meant just “all legal moves” (and 19x19), not “a game that could plausibly happen between two skilled players trying to win”, which is of course very hard to define.
They also specified “no handicap”, I’m going to discuss why later.
But then they specified they meant “capture with a single move”, not throughout the course of the game.
So, how many stones can be captured in a single move in a legal game of Go?
Note: throughout the post, we’re going to assume players have as many stones as they want to play with.
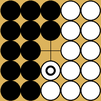
When pondering this question, I imagine everyone immediately thinks about a scenario like this:
So the question becomes, can you create a situation like this in a legal game? If this is possible, the answer to the question would be 360 (or N2–1 on a board of size NxN).
Without further restrictions, of course you can, and it’s pretty easy actually:
One of the two players just starts filling the board, and the other passes every move, until only one intersection remains on the board, at which point, the other player can capture all of the stones played so far. Here’s such a game.
If you were allowed handicap stones, I guess you could also have a game with N2–1 handicap stones and just capture them on the first move, which is why we had specified “no handicap” at the start.
So pretty uninteresting; a more interesting question is what if no player is allowed to pass and there’s no handicap?
What’s the maximum amount of stones you can capture in one move in a legal 19x19 Go game with no passes and no handicap?
The first thought you might get is that the answer might be around 180.
Capturing 180 stones is easy, for example you can just coordinate the two players to make two lumps of stones with no eyes:
but after Black plays on the Tengen and captures, the game can keep going, so that Black can build a bigger group that White can potentially capture at some point!
But how do we make it happen?
To avoid having to worry about eyes, and to avoid situations where the last liberty of a group doesn’t capture the other (and is thus illegal in most rulesets), I came up with this process where players always start as far away as possible, fill all the space by moving vertically, and fill the last column in a way that will lead to them “running into each other” at some point in the column.

So I’d like to see where this process leads, maybe it will show us the answer to our question.
Since I found it too difficult to think about the 19x19 board, at this point, I activated the good ol’ “make it simpler” trick, and started thinking about a 5x5 game instead.
On a 5x5 board, after the first capture, the process can keep going like this:
Here, suddenly White Uno-Reverses Black and captures all of the stones (the entire board minus 2) that Black had put together!
When I saw this, I initially thought “Alright, so the answer on a 19x19 is 361 – 2=359, right?”
But we would need to prove that the process would really happen the same way on a 19x19, and to do that, if it’s possible at all, we need to understand how the process really works.
Black kept capturing White several times, so how did White suddenly reverse the playing field? ![]()
Keeping the game going might provide some insight. After the big capture by White, the process gets to this point:
where Black goes back to being the one who captures, but then:
White reverses the capture again, but this time it’s very far from the corner! What is happening?
Thinking about it, I had the intuition that it must have something to do with parity. After all, who captures entirely depends on “who gets to fill the last liberty”, so let’s think about that.
The first capture in the entire game happens here by Black:
An even number of moves (24) happened before the capture. The game starts with Black-White-Black-White… this leads to Black being the first one to fill the last liberty.
When does the next capture happen?
Here:
Ok, let’s see, White was the first who got to play after being captured, so an odd number of moves has been played so far, and the Black capture happens on an even-numbered move relative to the previous capture. I don’t know, let’s skip ahead, to when the process reverses?
So Black captures, there are 3 spaces left, White gets to play first, and White wins.
Oh, of course we need to consider the number of spaces left, duh! ![]() That might be the key.
That might be the key.
So in the beginning the board has 25 spaces, Black goes first, Black wins the race – the same way that at the end White wins the race when there are 3 spaces left. How many spaces are there in the other cases?
In these cases, after the capture, there are 24 and 6 spaces left. Even number, White goes first, White loses.
So… what, if there’s an even number of spaces left, the player who gets to fill the last liberty is the one that goes second? Oh, wait…
Say the board is empty so there are 25 spaces left, Black plays first, there are 24 spaces left, White plays, so when Black plays there are 23 spaces left, so when White plays again, there are 22 spaces left…
We can see the process like this: b25, w24, b23, w22, b21, w20, b19, w18, b17…
When White plays, there are always an even number of spaces.
Who gets to capture? The one who gets to play when there’s only 1 space left, so odd! In this case Black.
So if there’s an even number of spaces left, the first player to go is the one who will get captured.
Whereas if there’s an odd number of spaces left, the first player to go is the one who will capture.
Note for any confused soul: this only applies to this specific process where the players mechanically keep playing this sequence of moves! It doesn’t apply generally to games of Go, obviously!
Since the first player to go is always the one who just got captured, this also means that whenever there’s an odd number of spaces left after a capture, the capturer and the captured switch roles for the next capture.
So, to better understand this process, it would be useful to have a way to predict when the next number is going to be odd or even.
Let’s see: when there’s an even number of spaces left, the players alternate filling them until they meet exactly in the middle.
https://online-go.com/api/v1/games/50376078/apng/50376078-37-43-500.png?from=37&to=43&frame_delay=500
^Here you can see it going from 6 spaces to 3.
This means the next capture is going to involve half the number of stones, or in other words that the next number of free spaces will be exactly half of the current one (since we know that the winner only flips if the number is odd, we can be sure of this).
Instead, when there’s an odd number of spaces, the winner flips and the process is a little more complicated, but let’s focus on the most important aspect: the players still alternate placing stones, which means that the capture will still happen pretty much in the middle, in fact it will happen exactly when the middle point of the “zig-zag segment” gets played.
Here, we have 5 spaces left:
https://online-go.com/api/v1/games/50376078/apng/50376078-139-139-500.png?from=139&to=139&frame_delay=500
And after both players have each filled 2 of them…
https://online-go.com/api/v1/games/50376078/apng/50376078-143-143-500.png?from=143&to=143&frame_delay=500
…White places the “middle stone” and flips the sequence.
https://online-go.com/api/v1/games/50376078/apng/50376078-144-144-500.png?from=144&to=144&frame_delay=500
So, the number of stones on the board after a “flip” capture has happened is always half the number of free spaces left after the previous capture, rounded up (an odd number divided by 2 will give a non-whole result).
In this case, there were 5 spaces left, halved gives 2.5, rounded up is 3, which is the number of White stones after the next capture.
And if that’s the number of stones on the board after the capture, then the number of spaces on the board after the capture is the board area minus that.
So on a board of size N, if O is the odd number of spaces left after a capture, the next number of spaces when the flip happens will be
N2 – roundUp(O/2)
Whereas, as we said earlier, if E is the even number of spaces left, the next number of spaces left will be simply
E/2
Well then, let’s apply this knowledge. On a 5x5 board, there are initially 25 spaces, which is odd, which is why Black wins. Then after the first capture, there are 25 – roundUp(25/2) = …
https://online-go.com/api/v1/games/50376078/apng/50376078-25-25-500.png?from=25&to=25&frame_delay=500
…12 spaces left – oh, crap, right. For those who don’t know, 12 is a “highly composite number”, and happens to have many factors of 2. It can be repeatedly divided by 2 until it results in a 3, which leads to the big capture (25 – roundUp(3/2)=23) we saw:
https://online-go.com/api/v1/games/50376078/apng/50376078-42-46-1000.png?from=42&to=46&frame_delay=500
I think it’s starting to look grim for our hopes of this happening on 19x19 too: such a big capture can only happen with a number with the properties of 12, specifically
Only a number which has all factors of two expect for perhaps a small odd number, like 3, can lead to such a “big capture” happening.
This also means that a capture of N2–1 can only happen if the process ever stumbles on a power of 2.
So, a sequence of numbers that needs to meet a power of two in order to be reduced to 1… somewhat reminiscent of the Collatz Conjecture, for those in the know; hopefully not as difficult to study though ![]()
Collatz Conjecture is that here all the numbers are bounded by N2.
(meaning they're all less than N2)
If we could prove that no number ever repeats twice, we could then use the "pigeonhole principle", or something equivalent, and that would prove that in at most N2 steps, the process will have ended up at N2-1.
But, don’t worry if you don’t understand what I just said, because I wasn’t able to prove it anyway ![]()
As far as I know, it might be possible for the process to get stuck in a cycle, for example oscillating between two different odd numbers A and B which happen to satisfy the equations
A = N2 – roundUp(B/2)
B = N2 – roundUp(A/2)
Is that possible?
To be honest I haven’t investigated too much, because now that we have a formula, we can try calculating value by value to see if it ever hits a power of 2…
...or I can just write a quick and dirty Python script.
B = 5 ** 2
capture = B // 2
sequence = []
for index in range(200):
sequence.append(capture)
if capture == B-1:
break
if capture%2 == 0:
capture = capture/2
else:
capture = B - capture//2 -1
print(sequence)
![]()
So here’s the output for size 5 (representing how many stones are captured each time):
[12, 6, 3, 23, 13, 18, 9, 20, 10, 5, 22, 11, 19, 15, 17, 16, 8, 4, 2, 1, 24]
Oh, there we go! This seems to indicate that on 5x5 a capture of 24 does indeed happen through this process! No pigeonholing required!
Of course let’s watch it happen; the process reaches a power of two at move 227, then at move 258 finally the climactic capture happens – it’s a snapback! (In case you hadn’t realized, as I didn’t before seeing it ![]() )
)
Then let’s do the same thing for 19x19:
[180, 90, 45, 338, 169, 276, 138, 69, 326, 163, 279, 221, 250, 125, 298, 149, 286, 143, 289, 216, 108, 54, 27, 347, 187, 267, 227, 247, 237, 242, 121, 300, 150, 75, 323, 199, 261, 230, 115, 303, 209, 256, 128, 64, 32, 16, 8, 4, 2, 1, 360]
The python script tells us the big capture should indeed happen, and generating the game we can see it in action:
A neat thing about both of these situations, by the way, is that, as I said before, this big capture can only happen if the process stumbles on a power of two at some point; and in both of these situations, not only does it happen, but the power of two is the largest possible on the relative board:
[12, 6, 3, 23, 13, 18, 9, 20, 10, 5, 22, 11, 19, 15, 17, 16, 8, 4, 2, 1, 24]
[180, 90, 45, 338, 169, 276, 138, 69, 326, 163, 279, 221, 250, 125, 298, 149, 286, 143, 289, 216, 108, 54, 27, 347, 187, 267, 227, 247, 237, 242, 121, 300, 150, 75, 323, 199, 261, 230, 115, 303, 209, 256, 128, 64, 32, 16, 8, 4, 2, 1, 360]
A kink to fix, though, is that in both of these situations, if the game had started on the upper left corner, superko rules would prevent the snapback to happen ![]()
But it’s easy enough to avoid by choosing the corners carefully. In this case, I chose to start the game from the lower corner, and on 5x5 too.
To go further, since the process is mechanical, it’s easy to prove that as long as that specific quirk is avoided, any other position in the game doesn’t break situational superko:
If SSK was broken, it would mean a cycle is happening and all the following moves would be the same, which means the same situation can’t happen twice before the ending capture, because if it happened twice, it would be a cycle, so the game would just loop ad infinitum and the ending capture would never happen.
Positional superko is trickier, because the same position could happen with a different player to move. In fact, since the process tends to create the same kind of position over and over, it seems quite likely.
Didn’t take me long to find an example:
https://online-go.com/api/v1/games/50376078/apng/50376078-26-26-500.png?from=26&to=26&frame_delay=500
https://online-go.com/api/v1/games/50376078/apng/50376078-71-71-500.png?from=71&to=71&frame_delay=500
moves 26 and 71 of the game produce the same position, but the player to play is different.
We need to avoid this, or at least find out if it happens on 19x19. So we need a way to study positional repetitions more easily.
The first thing I notice that goes to our advantage is that the same position can only happen in one of two situations (Black to play, White to play).
For the same reasoning we used for situational superko, we know each of these two situations can only happen once, or it would lead to a cycle, which we know can’t happen before the first time the big capture happens.
Here’s the insight that helped me move forward: since the stone structure, without superko-preventative modifications, is always the same, any situation that happens is only characterized by three parameters: how many Black stones, how many White stones, which player has to play.
For example, the two situations considered above:
https://online-go.com/api/v1/games/50376078/apng/50376078-26-26-500.png?from=26&to=26&frame_delay=500
https://online-go.com/api/v1/games/50376078/apng/50376078-71-71-500.png?from=71&to=71&frame_delay=500
could be parametrized as (13,1,B) and (13,1,W).
And as soon as I looked at this, I thought: “These look an awful lot like Cartesian coordinates”
Since we need to study positional superko, let’s just focus on the number of stones and ignore the B/W parameter – if you don’t understand why, just go with the flow, you’ll see ![]()
At the start of the game, there are no stones, so the initial position is (0,0).
Then Black puts down a stone, and we’re at (1,0).
Then White puts down a stone, and we’re at (1,1). And so on.
If we plot this, we can look at the process:

Every movement to the right is a Black move, every movement up is a White move.
So in this “parameter space”, the process of filling the board draws something like a set of stairs, or like a Go ladder if you wish.
But what do captures look like on the graph?
Well, if you think about it, in our process, the move that captures is always the one that would “fill the board” (if the capture didn’t happen).
What I mean is, it’s impossible to have the board completely filled with stones of two different colors, so when the “ladder” reaches the point where x+y=N2, the capture happens and one of the two coordinates is reset to zero (the one representing the captured color of course).
Just to picture it more clearly, here’s the process on a 3x3 board:
https://online-go.com/api/v1/games/50528237/apng/50528237-1-16-500.png?from=1&to=16&frame_delay=500
And here’s how the graph for it starts:
When the process “bumps against” the x+y=9 line, it can’t go on (because it would fill the board, exhausting all liberties), so 1 black is added (x increases by 1), but all the white stones are captured (y decreases to 0). And so on multiple times.
Incidentally, on a 3x3 board the “climactic” capture happens pretty much immediately; in the above graph I didn’t represent it just to make it cleaner, but here it is in green:
Alright, so, can we use this to study positional superko?
Well, let’s just see what happens if we keep the game going. After White captures all the Black stones, it’s Black’s turn, so:
Aha! The new “ladder” is too close to the previous one, so it has to overlap it. But since it didn’t start from the same position, this doesn’t break situational superko, only positional superko.
We can see this in action on the board:
https://online-go.com/api/v1/games/50528237/apng/50528237-1-24-500.png?from=1&to=24&frame_delay=500
Here’s a slower version if you want to study it more carefully and compare it to the graph above:
https://online-go.com/api/v1/games/50528237/apng/50528237-1-24-500.png?from=1&to=24&frame_delay=1200
Here’s a comparison of move 2 and move 17:
https://online-go.com/api/v1/games/50528237/apng/50528237-2-2-500.png?from=2&to=2&frame_delay=500
https://online-go.com/api/v1/games/50528237/apng/50528237-17-17-500.png?from=17&to=17&frame_delay=500
And then, in case you didn’t realize until now, the repetitions keep happening every two moves until a capture happens:
https://online-go.com/api/v1/games/50528237/apng/50528237-4-4-500.png?from=4&to=4&frame_delay=500
https://online-go.com/api/v1/games/50528237/apng/50528237-19-19-500.png?from=19&to=19&frame_delay=500
(but when the two overlapping ladders reach the point of capture, the captured color is different, represented by the long arrows going in different directions in the graph)
Now you might be wondering, why did I only show it on 3x3? Isn’t it possible that the only reason the process came back that way was because the big capture happened?
Well, it being on 3x3 does influence the “ladder” overlap to happen exactly that way, but it’s possible for “ladders” to overlap on bigger boards even before the big capture. I could try to find a mathematical arguments, but I guess it’s easier just to show an example.
The only reason I did the graph on 3x3 so far is because it gets really big really fast, and already on 5x5 it’s kinda difficult to read and annoying to draw out ![]()
But here’s how it starts, until the first conflict happens:
Some help to read this graph:
- as a reminder, the process starts at 0;
- the point (13,1) (13 horizontal, 1 vertical) is also where the positional repetition that I had manually found happens, corresponding to 13 black stones and 1 white stone on the board;
- the capture that happens first after the (18,6) point is the longer dotted arrow that moves to the right, going to (19,0).
Well, actually, all of this was just to have a visual and make things a bit more concrete, but really, all we need to know is that it’s possible to represent the states of the board with XY coordinates, and a positional repetition is just the process hitting the same point twice, though from different angles.
So now I could start trying to find a mathematical way to prove whether or not repetitions happen on a board of size NxN…
…but I can just use Python again to find all of the repetitions of coordinates ![]()
(Code)
size = 5
param = [0,0]
moves = []
conflicts = []
pastFirstMove = False
for index in range(100000):
param[index%2] += 1
if sum(param) == size**2:
param[(index+1)%2] = 0
if param in moves:
conflicts.append(param.copy())
moves.append(param.copy())
if pastFirstMove and sum(param) == 1:
break
pastFirstMove = True
print(conflicts)
This is the output for 5x5:
[[13, 1], [14, 2], [15, 3], [16, 4], [17, 5], [18, 6], [20, 1], [21, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7], [6, 8], [7, 9], [8, 10], [9, 11], [10, 12], [11, 13], [6, 1], [7, 2], [8, 3], [9, 4], [10, 5], [11, 6], [12, 7], [13, 8], [14, 9], [1, 10], [2, 11], [3, 12], [4, 13], [5, 14], [6, 15], [7, 16], [1, 17], [2, 18], [3, 19], [4, 20], [1, 0]]
So if we wanted to readapt this process for 5x5, we’d need to find a way to avoid the positional superko every time the number of stones on the board is the same.
But before thinking about that, let’s brace ourselves and see what the output is for 19x19:
[[1, 0]]
![]()
wut
That’s just the first move. You know, this one:
https://online-go.com/api/v1/games/50371099/apng/50371099-9150-9151-500.png?from=9151&to=9151&frame_delay=500
which, if we don’t take precautions, also repeats after the big capture, as discussed earlier:
https://online-go.com/api/v1/games/50371099/apng/50371099-9130-9151-500.png?from=9130&to=9151&frame_delay=500
So as long as we take care to avoid the same situational superko, by for example starting the game in the lower corner instead of the upper one, it’s all solved?
That’s crazy.
But thinking about it, like in the XY graph, maybe it makes sense, right? The graph gets bigger and bigger, so the probability of a conflict arising should get lower and lower. What’s the chance two “ladders” will happen to fall right next to each other in a huge graph, right?
Well, I was curious, so I adapted the code to do the calculation for all these board sizes.
for size in range(3,26):
param = [0,0]
moves = []
conflicts = []
pastFirstMove = False
for index in range(100000):
param[index%2] += 1
if sum(param) == size**2:
param[(index+1)%2] = 0
if param in moves:
conflicts.append(param.copy())
moves.append(param.copy())
if pastFirstMove and sum(param) == 1:
break
pastFirstMove = True
print(f'{size}x{size}: {len(conflicts)}')
| Size | Positional Repetitions |
|---|---|
| 3x3 | 0 |
| 4x4 | 1 |
| 5x5 | 40 |
| 6x6 | 126 |
| 7x7 | 51 |
| 8x8 | 1 |
| 9x9 | 65 |
| 10x10 | 1307 |
| 11x11 | 7 |
| 12x12 | 324 |
| 13x13 | 1 |
| 14x14 | 614 |
| 15x15 | 1527 |
| 16x16 | 1 |
| 17x17 | 568 |
| 18x18 | 12686 |
| 19x19 | 1 |
| 20x20 | 3295 |
| 21x21 | 1 |
| 22x22 | 20905 |
| 23x23 | 1 |
| 24x24 | 16120 |
| 25x25 | 1643 |
Huh. Ok, I understand why 4, 8 and 16 don’t give conflicts, since they’re powers of two (see above stuff when I talked about powers of two ![]() ). But other than that, 13, 19, 21 and 23 are just the “odd ones out”, apparently.
). But other than that, 13, 19, 21 and 23 are just the “odd ones out”, apparently.
A few interesting things to note:
- other than 4, 8 and 16, no other even-sized boards avoid positional superko before the final capture.
- No size other than 3 has 0 repetitions. This might mean that in all these boards except 3x3 the final capture happens with Black capturing all the White stones, but I’d need further checking to make sure.
- To the chagrin of 9x9 fans, I imagine, the 9x9 board is the only one with many positional repetitions, out of the three “standard” sizes.
Anyway, I’m digressing. We did find our answer!
If we just start the game from anywhere other than the upper left corner, to avoid that positional repetition, but otherwise apply this process mechanically, on a 19x19 board it will eventually (at move 9151) result in a capture of 360 stones, and the process, by some miracle, doesn’t break positional superko anywhere along the line!
Since it’s obviously impossible to capture 361 stones in one move on 19x19, this means
the maximum amount of stones you can capture in one move in a legal 19x19 Go game with no passes and no handicap is 360.
A few remarkable things about this game we found:
-
the process requires hitting a power of two in order to lead up to the big capture, and in this game it hits the largest possible power of two (the largest that is still smaller than 361) at 256, at move 8640.
-
as pointed out, just the naive process itself would completely avoid positional superko, were it not for the very move we’re interested in

And to finish, a few questions for people who are better at mathematics and less burnt out than I am:
-
Is there a way to prove that the N2–1 capture does happen for a board of size N with the process described above (i.e. without having to check manually), both in general or for some specific sizes?
-
Is there a way to mathematically study the positional repetitions without manually checking for them the way I did?
-
In the boards where those repetitions happen, for example 9x9, is there a good way to define a modification of the mechanical process to avoid the repetitions?
-
And the same question I glossed over in the beginning, what if instead of “how many stones in a single capture” we wanted to study “how many prisoners can you capture throughout a game of Go” and we wanted to avoid superko? Is there a good way to study that?
Well, I’m finally free. I’ve been writing this for a long time ![]()
Let the peer review start, if the peers wish to review.
Edit: how could I forget!
Acknowledgements:
@_KoBa helped me with the first part of this proof, and generally supported and encouraged the production of this text. Thank you! ![]()
@sfas was the one who first came up with the question here, and probably helped with the initial reasoninig too, it was a while ago so I don’t remember ![]()