Correct!
Well, it doesn’t kill, locally it’s a seki 
(but black is out of moves, so is forced to suicide next, so in that sense I guess it kills)
To summarise the solution: black needs to start with D2 to prevent white from securing an extra point with this 8:
Like you noted above, your correct variation is very similar to this, but sort of forcing white to play D3 instead of D2, which loses a point. I think this problem is so difficult because it’s all about taking a key point from the opponent, but you can’t see that it’s a key point without reading 8 moves ahead!
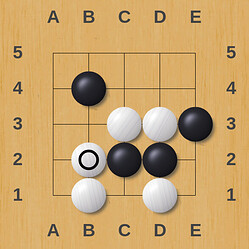
He he the funny thing in this variant is that two eyes are not necessary to live, one eye with two adjacent intersections is sufficient 
Let’s take a little break from the normal problems after this first batch of 10, and instead consider this:
Problem A
Assume for this problem that passes are allowed. Can you construct a position such that:
- Regardless of whose turn it is, the only winning move is passing.
- Both black and white have available moves which are neither suicide nor self-atari (so after the move, all their chains have at least 2 liberties).
Some background on this problem
I sort of hoped that the answer was “no”, since this would allow a certain endgame-optimisation in a solver I’m working on. But after some thinking I actually found a position with the above properties. I’m interested to see if someone comes up with a significantly different position, or if all solutions will be similar.
I’m interrested, but I feel like I’m either misunderstanding the rules, or this is contradictory. If passing is a winning move regardless of who is on the play, wouldn’t both players endlessly play passes? Which player wins in such a scenario?
Assume if you want that if both players pass, it’s a draw. (in the context of the solver, both sides passing would rather signify that we enter a special “counting” phase, where the order of moves doesn’t matter; both players will just fill up their territory).
But we don’t have to worry about what happens if both players pass, the task is to construct a position where if black is forced to play first, white will be able to capture black, and vice versa. An obvious example of this would be a basic seki between two groups with one eye and one shared liberty, but filling the shared liberty is a self-atari so this doesn’t satisfy the 2nd criterion.
So in loose terms the question can be restated as, can you find a seki-like position, where the chains involved have more than 2 liberties?
So if I understand correctly, passing is generally not allowed, but we should construct a position where either side would want to give the opponent the move. In chess terms we would call that “Zugzwang”. Is this what you mean?
Yes, that’s basically it! Are there Zugzwang positions apart from the obvious ones where all chains have two liberties?
I stated it in terms of passes being allowed, because if you just consider the question above, then two groups with two eyes each and two shared dame also seems to be a solution. Both sides would rather pass, but it doesn’t hurt to exchange one dame for the other first. The sort of positions I’m looking for are such that passing immediately is the only winning move; playing once and then passing after that won’t work, you will be captured.
Yeah, this is an excellent demonstration of what I just wrote at the same time you posted it 
Here, if we assume that passes are allowed, and both sides passing is a draw, then this would be a draw regardless of whether you play a dame first or pass first.
I’m looking for a position where if you’re forced to play first, you can’t escape capture, even with the help of passes.
Oh I’m sorry, I should have read your message more carefully.
Edit: At the risk of being pedantic here, with passes allowed the statement
should (im my opinion) instead be:
“Regardless of whose turn it is, passing is the only move that does not lose.”
Yeah you’re right, I defined the problem clumsily. The idea of two passes being a draw wasn’t something I had in mind when writing it, but that’s probably the easiest way to explain what I’m looking for.
Hopefully it’s clarified now. If not it should be clear once I share my solution, but I’ll let you think about it first to increase the chances that you come up with something completely different 
Spoiler
Yup, that’s the one I came up with as well
It obviously generalizes to circular sekis with 6, 8 etc groups. But is there some solution which doesn’t involve such a seki? I haven’t found one yet.
Hm …
spoiler
I briefly looked-up the definition of Seki at Sensei’s Library, which includes:
" … two live groups share liberties which neither of them can fill without dying."
If I’m not mistaken, the positions of interest have to involve a Seki by definition. Well maybe not if you stick to the narrow definition of Seki, but I prefer a more general definition, for example “Seki ~ mutual life. Any attempt to capture the opponents group gets your own group captured”.
Spoiler
Yeah, you may be right that any solution will be seki by definition (depending on the definition). But there are (at least in regular go) many different types of seki. This is a very particular type: 2n groups (n > 1) in a cycle, each with exactly one eye and one shared liberty with both of its neighours. It would be interesting to know whether this is the only possible situation where both sides would like to pass despite having non-suicidal moves (well, the moves are of course suicidal, but they aren’t immediately suicidal). For now I’m leaning towards yes, but I haven’t attempted to prove it
